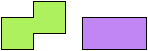
Two-sided polynars may be rotated and reflected. One-sided polynars may be rotated but not reflected.
Polynars were first studied by László Molnár. Previously, around 2004, Saturo Natsuki (夏木智) invented some puzzles using pieces made with three cubes—three-dimensional trinars.
| Order | Two-Sided | One-Sided |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 9 | 13 |
| 4 | 60 | 112 |
| 5 | 467 | 896 |
| 6 | 4226 | 8381 |
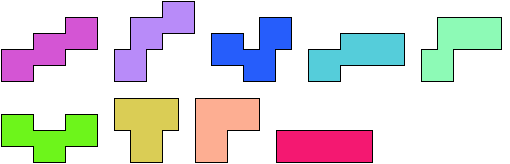
The figures below show two-sided polynars.