Catalogue of Polykedges

Introduction

Polyforms can be made from equal cubes by joining them face to face, edge to edge, vertex to vertex, or any combination of these. A polykedge is formed by joining equal cubes at faces or edges or both. Polykedges include polycubes, which are joined face to face, and polyjubes, which are joined edge to edge.

Here I show all polykedges with at most 4 cells. Like polycubes, polykedges may be one-sided or two-sided. One-sided means that distinct mirror images are counted as different polykedges. Two-sided means that distinct mirror images are counted as the same polykedge.

Enumeration

Cells	Two-Sided A268666	One-Sided A270862
1	1	1
2	2	2
3	8	9
4	64	88
5	646	1103
6	9364	17570
7	151028	295506

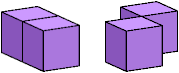
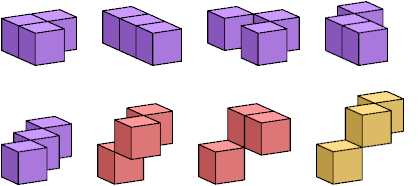
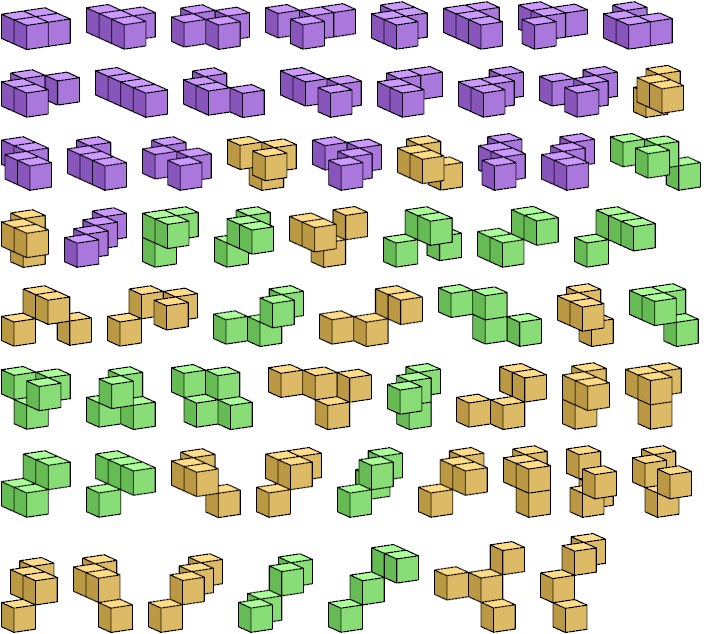
The diagrams below show two-sided polykedges. Flat polykedges are shown in purple; these are the solid polykings. Polykedges with distinct mirror images are shown in yellow; these are the chiral polykedges.

Monokedge

Dikedges

Trikedges

Tetrakedges

Last revised 2020-11-13.

Back to Polyform Catalogues < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]