Scott Reynolds first studied pentapent compatibility and found most of the early solutions.
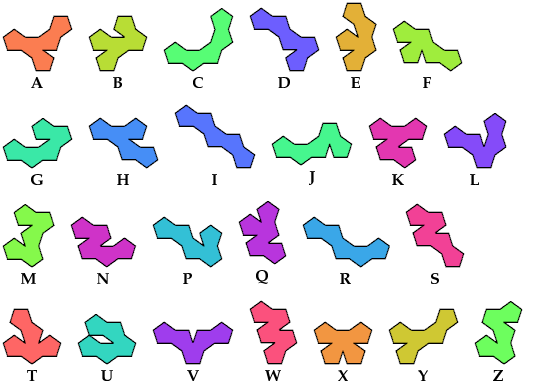
I adopt Erich Friedman's nomenclature:

| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 4 | 4 | 2 | 10 | 5 | 5 | 5 | 5 | 2 | 5 | 5 | 5 | 5 | 6 | 2 | 2 | 2 | 5 | 5 | 2 | × | 2 | 2 | 5 |
| B | 4 | * | × | 2 | 6 | 6 | 5 | 2 | × | 2 | 5 | 5 | 5 | 5 | 2 | × | × | 2 | 2 | 5 | 5 | × | 10 | 3 | 4 |
| C | 4 | × | * | 2 | 2 | × | 2 | 5 | 5 | 4 | 4 | 2 | × | 10 | 8 | 5 | 2 | 5 | 5 | 4 | 10 | × | × | 5 | × |
| D | 2 | 2 | 2 | * | 5 | 4 | 2 | 2 | 4 | 4 | 4 | 2 | 2 | 4 | 2 | 2 | 2 | 5 | 5 | 4 | 2 | 5 | × | 2 | 4 |
| E | 10 | 6 | 2 | 5 | * | 5 | 5 | 5 | × | 4 | 6 | 2 | 5 | 5 | 5 | 4 | 4 | × | 3 | 6 | ? | ? | 6 | 6 | 5 |
| F | 5 | 6 | × | 4 | 5 | * | 5 | 10 | 4 | 5 | ? | 6 | 2 | × | 5 | 2 | 2 | 5 | 3 | 10 | 2 | ? | 2 | 2 | 4 |
| G | 5 | 5 | 2 | 2 | 5 | 5 | * | 5 | 2 | 5 | 5 | 2 | 5 | 2 | 2 | 4 | 2 | 6 | 5 | 2 | 4 | 2 | × | 4 | 4 |
| H | 5 | 2 | 5 | 2 | 5 | 10 | 5 | * | 2 | 5 | 2 | 2 | ? | 2 | 4 | ? | 4 | 2 | 5 | 6 | 5 | ? | 6 | 4 | 5 |
| I | 5 | × | 5 | 4 | × | 4 | 2 | 2 | * | 4 | 2 | 4 | ? | 2 | 2 | ? | 2 | 8 | 5 | 2 | 6 | 10 | × | 2 | 10 |
| J | 2 | 2 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | * | 5 | 6 | 4 | 5 | 4 | 2 | 4 | 2 | 2 | 15 | 2 | 4 | × | 4 | 4 |
| K | 5 | 5 | 4 | 4 | 6 | ? | 5 | 2 | 2 | 5 | * | 5 | ? | 4 | 2 | 5 | 5 | 2 | 5 | 5 | ? | 2 | 10 | 4 | 2 |
| L | 5 | 5 | 2 | 2 | 2 | 6 | 2 | 2 | 4 | 6 | 5 | * | 2 | 5 | 2 | 5 | 2 | 5 | 5 | 5 | 2 | ? | × | ? | 6 |
| M | 5 | 5 | × | 2 | 5 | 2 | 5 | ? | ? | 4 | ? | 2 | * | 4 | 2 | 10 | ? | 4 | 5 | ? | 2 | ? | × | 2 | 5 |
| N | 5 | 5 | 10 | 4 | 5 | × | 2 | 2 | 2 | 5 | 4 | 5 | 4 | * | 4 | 4 | 4 | 4 | 6 | 5 | 6 | 2 | × | 10 | 4 |
| P | 6 | 2 | 8 | 2 | 5 | 5 | 2 | 4 | 2 | 4 | 2 | 2 | 2 | 4 | * | 5 | 2 | 4 | 5 | 2 | 2 | 2 | × | 4 | 4 |
| Q | 2 | × | 5 | 2 | 4 | 2 | 4 | ? | ? | 2 | 5 | 5 | 10 | 4 | 5 | * | ? | 2 | 5 | 5 | 5 | 5 | 2 | ? | 5 |
| R | 2 | × | 2 | 2 | 4 | 2 | 2 | 4 | 2 | 4 | 5 | 2 | ? | 4 | 2 | ? | * | 2 | 5 | 2 | 2 | 10 | 10 | 2 | 30 |
| S | 2 | 2 | 5 | 5 | × | 5 | 6 | 2 | 8 | 2 | 2 | 5 | 4 | 4 | 4 | 2 | 2 | * | 5 | 10 | 5 | 4 | × | 5 | 2 |
| T | 5 | 2 | 5 | 5 | 3 | 3 | 5 | 5 | 5 | 2 | 5 | 5 | 5 | 6 | 5 | 5 | 5 | 5 | * | 5 | 5 | × | 6 | 4 | 5 |
| U | 5 | 5 | 4 | 4 | 6 | 10 | 2 | 6 | 2 | 15 | 5 | 5 | ? | 5 | 2 | 5 | 2 | 10 | 5 | * | 6 | × | 10 | 8 | 6 |
| V | 2 | 5 | 10 | 2 | ? | 2 | 4 | 5 | 6 | 2 | ? | 2 | 2 | 6 | 2 | 5 | 2 | 5 | 5 | 6 | * | × | × | ? | 6 |
| W | × | × | × | 5 | ? | ? | 2 | ? | 10 | 4 | 2 | ? | ? | 2 | 2 | 5 | 10 | 4 | × | × | × | * | × | 2 | 10 |
| X | 2 | 10 | × | × | 6 | 2 | × | 6 | × | × | 10 | × | × | × | × | 2 | 10 | × | 6 | 10 | × | × | * | 2 | × |
| Y | 2 | 3 | 5 | 2 | 6 | 2 | 4 | 4 | 2 | 4 | 4 | ? | 2 | 10 | 4 | ? | 2 | 5 | 4 | 8 | ? | 2 | 2 | * | 4 |
| Z | 5 | 4 | × | 4 | 5 | 4 | 4 | 5 | 10 | 4 | 2 | 6 | 5 | 4 | 4 | 5 | 30 | 2 | 5 | 6 | 6 | 10 | × | 4 | * |






Last revised 2018-03-10.