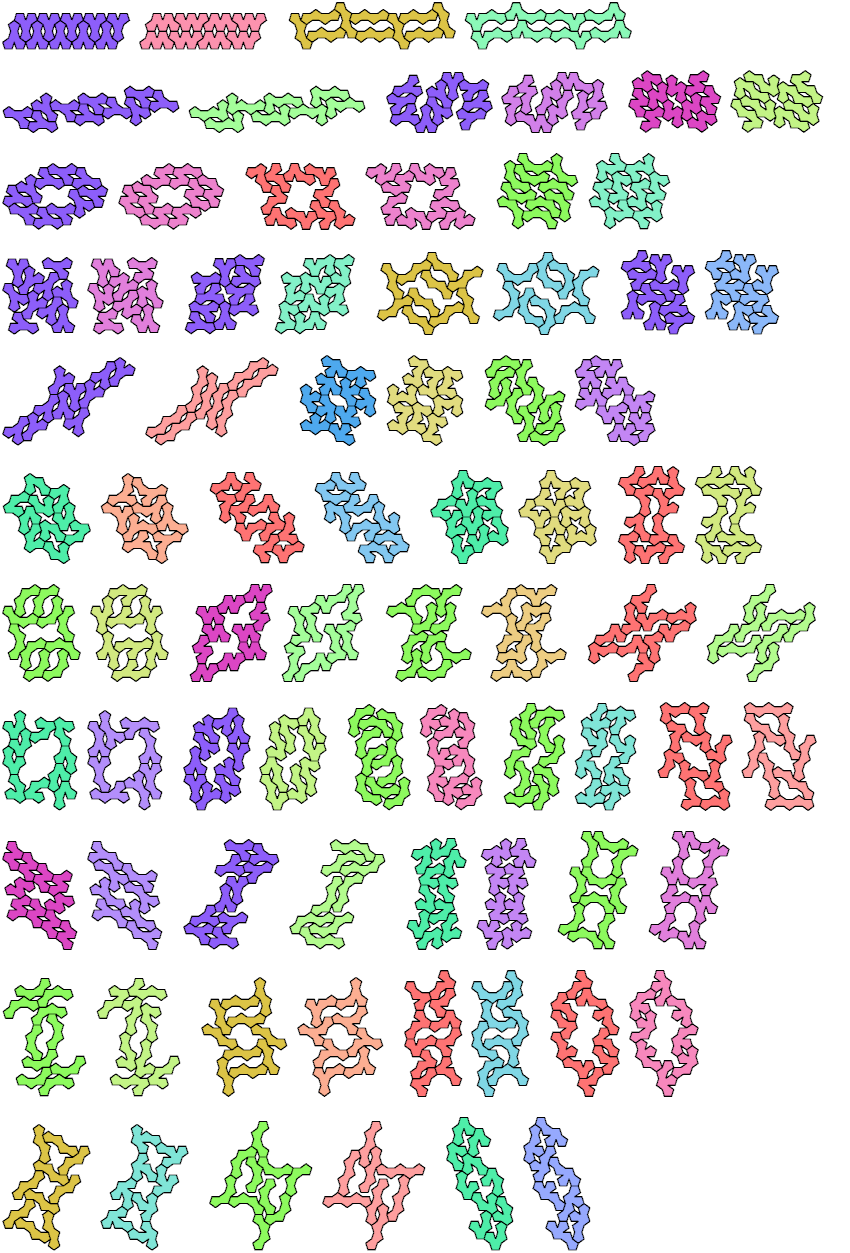
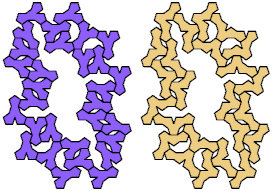
Two or more polyforms are said to be compatible if there exists a figure that can be tiled with any of them. Here I present some compatibility figures for tetrapent-pentapent pairs.
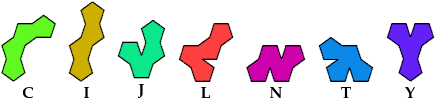
Here are the 7 tetrapents:

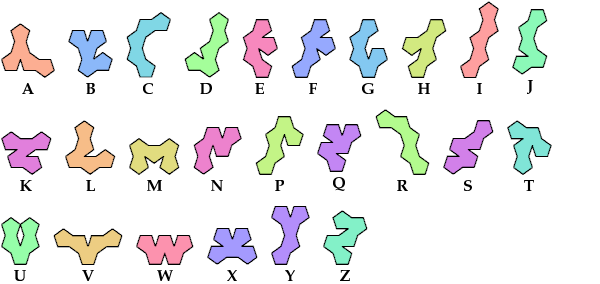
I adopt Erich Friedman's nomenclature for the 25 pentapents:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | 4 | 16 | 4 | 4 | 8 | 20 | 4 | 8 | 8 | 4 | 8 | 4 | 20 | 4 | 8 | 8 | 4 | 4 | 8 | 16 | 8 | 4 | ? | 4 | 8 |
| I | 8 | 16 | 8 | 4 | 16 | ? | 4 | 4 | 4 | 8 | 4 | 4 | ? | 4 | 4 | 16 | 4 | 4 | 8 | 4 | 16 | 4 | ? | 4 | 4 |
| J | 8 | 4 | 4 | 4 | 4 | 8 | 4 | 4 | 4 | 4 | 4 | 4 | 8 | 4 | 4 | 8 | 4 | 4 | 4 | 4 | 4 | 16 | ? | 8 | 4 |
| L | 4 | 4 | 8 | 4 | 8 | 4 | 8 | 8 | 8 | 4 | 16 | 4 | 4 | 8 | 4 | 4 | 8 | 4 | 4 | 20 | 4 | ? | ? | 4 | 4 |
| N | ? | 16 | ? | 8 | 16 | ? | 4 | ? | 4 | 16 | 4 | ? | ? | 4 | 8 | 4 | 4 | 4 | ? | ? | ? | 4 | ? | 8 | 16 |
| T | 16 | 20 | 20 | ? | 4 | 4 | ? | ? | ? | 4 | ? | 80 | 8 | ? | ? | 4 | 40 | ? | 4 | ? | ? | ? | 4 | ? | ? |
| Y | 4 | 8 | ? | 8 | ? | 16 | ? | 4 | 8 | 16 | 8 | 16 | 16 | 8 | 8 | ? | 8 | 8 | ? | ? | 24 | 8 | ? | 4 | 8 |



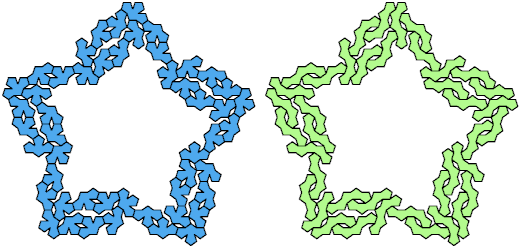
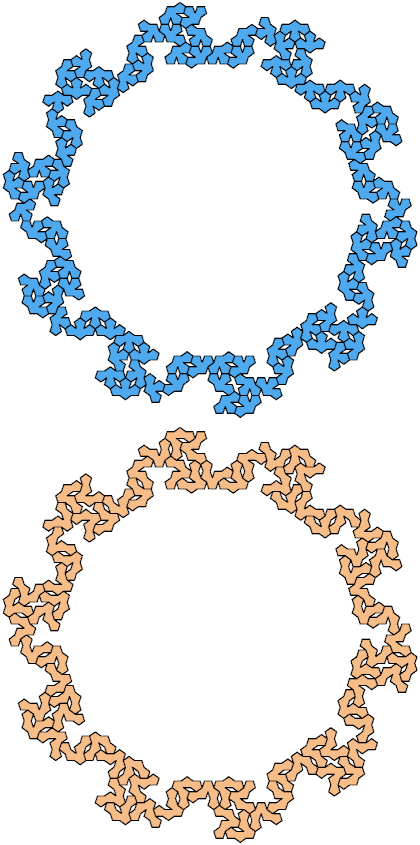
Last revised 2023-12-03.