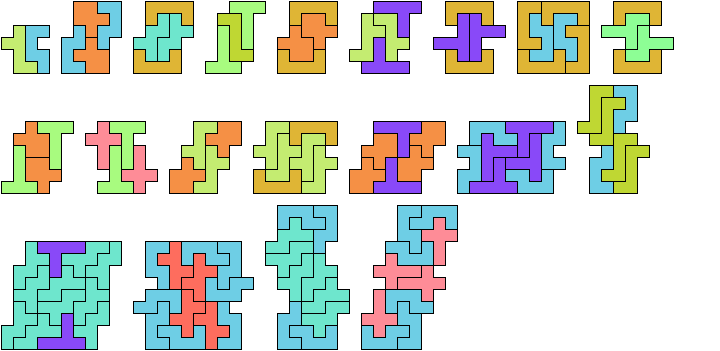
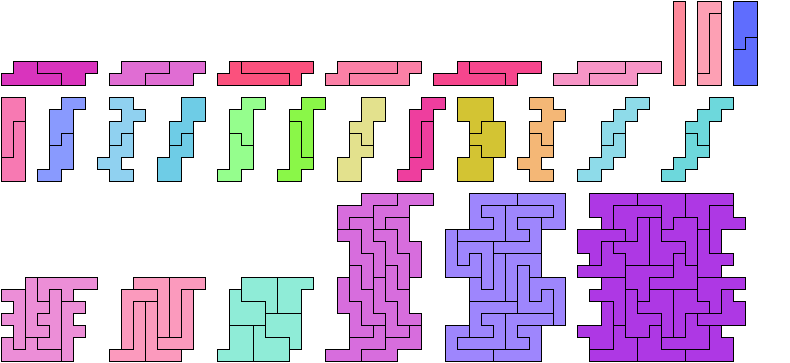
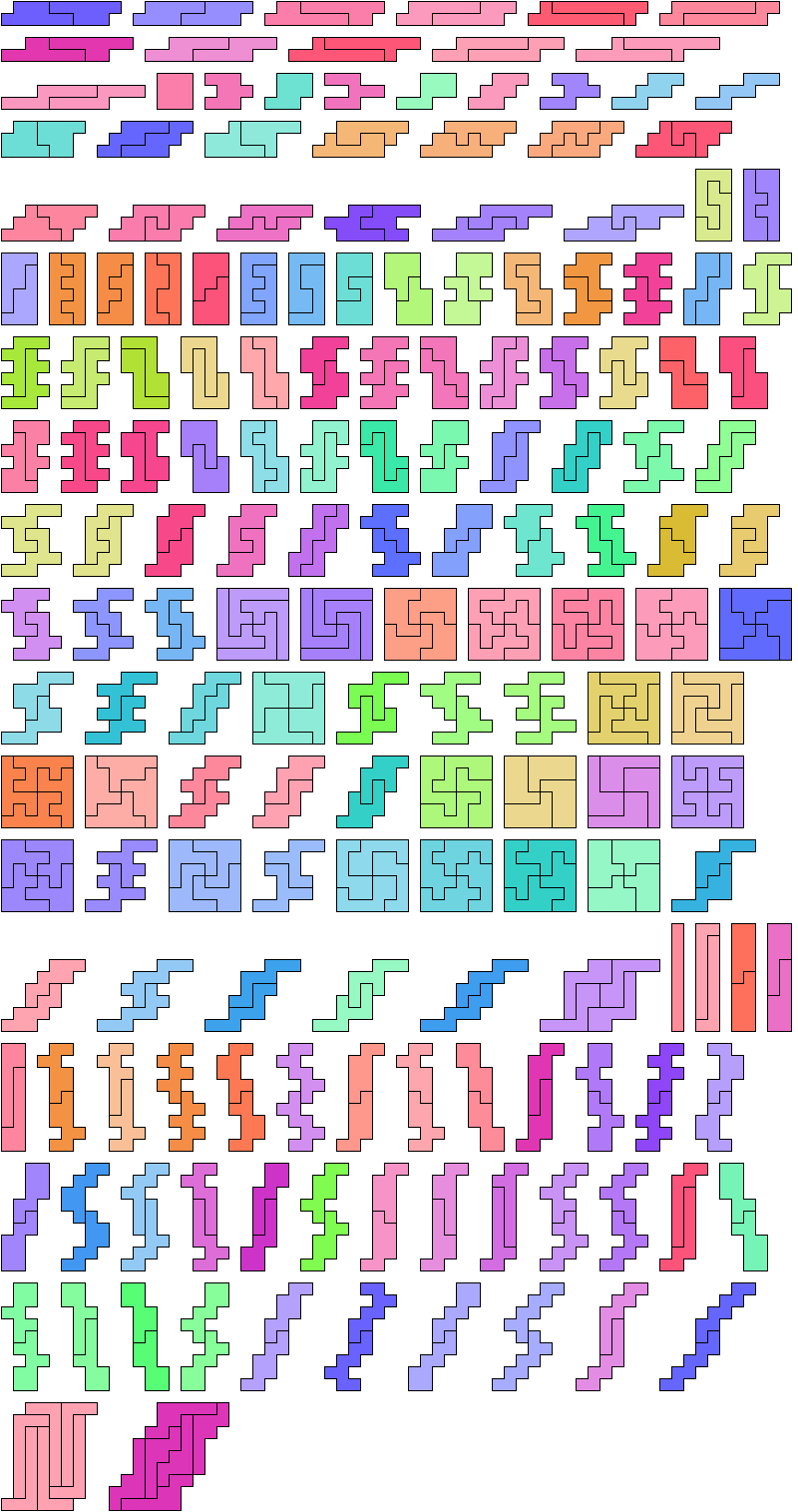
Uniform Polyomino Stacks
A uniform polyomino stack is a figure
formed by joining copies of a polyomino, having the same
contiguous length of cells in every row.
Such a figure is compatible with every linear polyomino.
It is equivalent to a tiling of a cylinder, but not every
cylindrical tiling defines a uniform stack.
Here are minimal known uniform stacks for polyominoes
of orders 1 through 9.
If you find a smaller solution or solve an unsolved case,
please write.
See also Uniform Polyiamond Stacks.



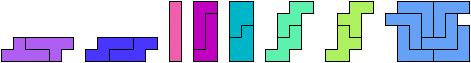
Impossible

Hybrid Solutions


Impossible

Hybrid Solutions

Last revised 2023-06-28.
Back to Polyform Tiling
<
Polyform Curiosities
George Sicherman
[ HOME
| MAIL
]