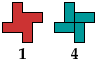
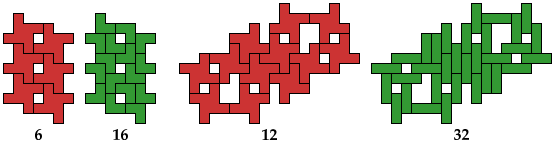
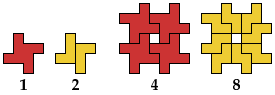
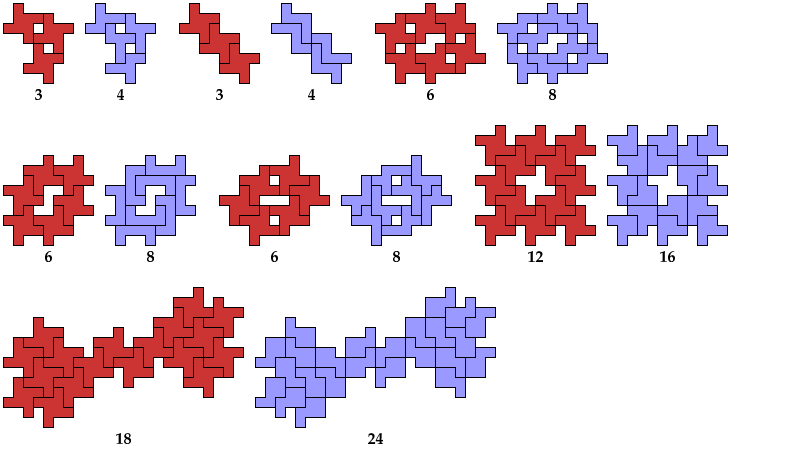
The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Here I show minimal known compatibility figures for the pinwheel octomino and other polyominoes. If you find a smaller solution or solve an unsolved case, please let me know.
All but one of the solutions for trominoes, tetrominoes, and pentominoes were found by Giovanni Resta and can be seen at his monumental website Polypolyominoes.
Mark Smith suggested this page.
{ Domino | Trominoes | Tetrominoes | Pentominoes | Hexominoes | Heptominoes | Octominoes | Enneominoes }




Last revised 2016-02-26.