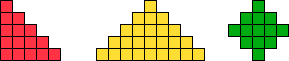

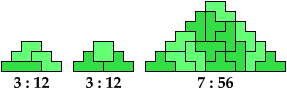
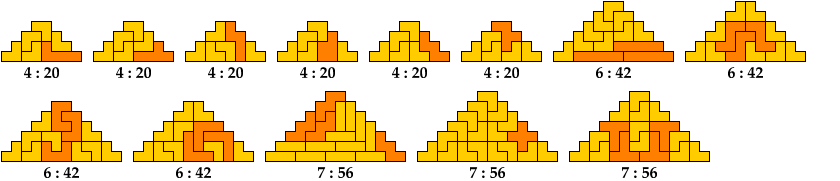
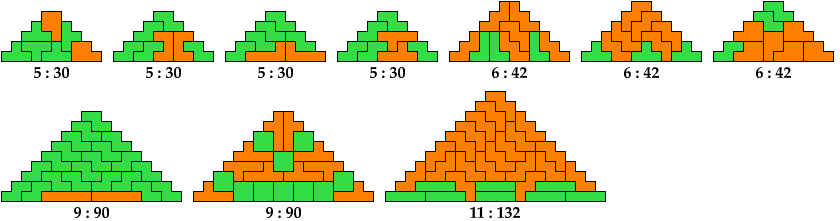
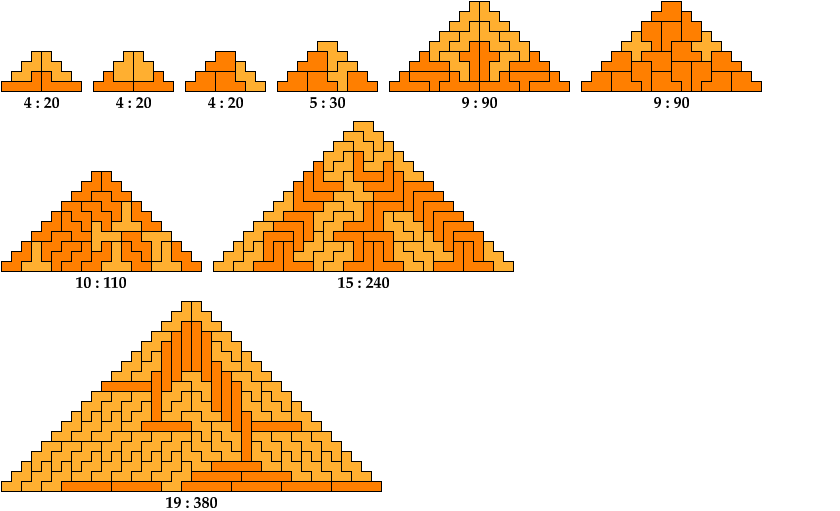
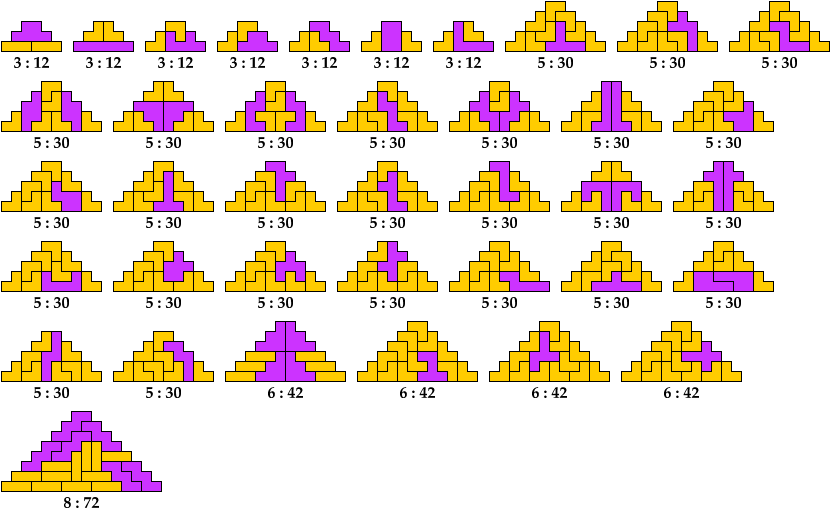
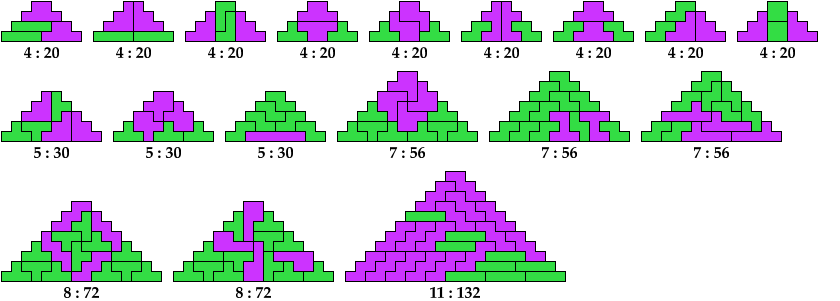
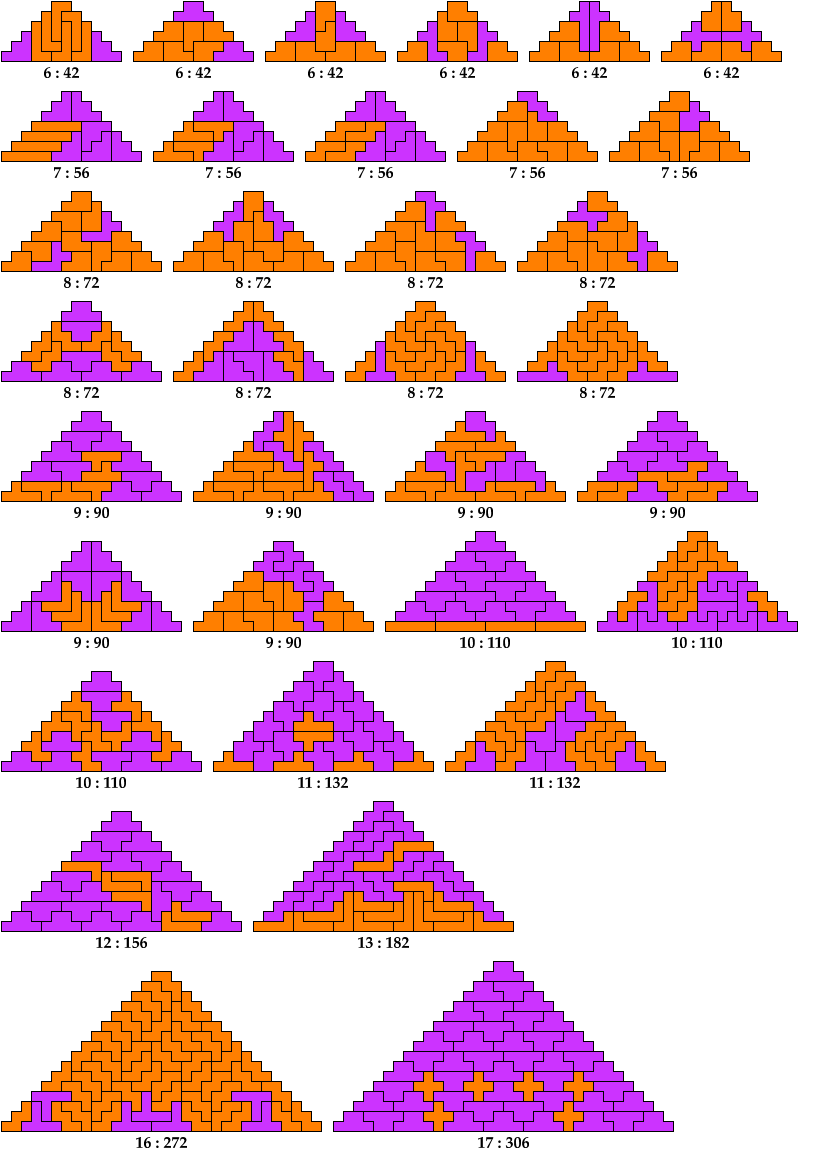
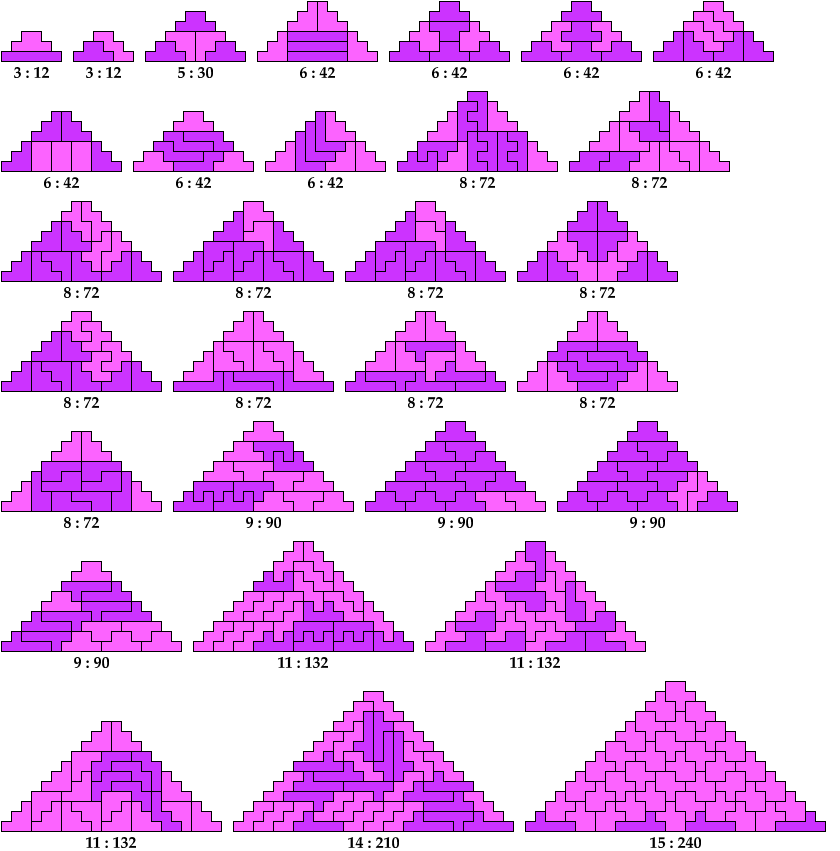
Below I show minimal known pyramids with two cells at the apex that can be tiled by two given polyominoes. Unlike such shapes as those shown above, blunt pyramids have balanced cell parity. They can be tiled by some pairs of polyominoes with balanced cell parity.
Any pair of polyominoes that can tile a triangular polyomino, such as the red polyomino above, can tile a blunt pyramidal polyomino.
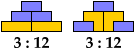
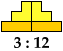
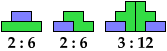
Shown below each tiling are its height and area.
I omit pairs in which one polyomino is the monomino.
| 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|
| 3 | @ | @ | ||||
| 4 | @ | @ | @ | |||
| 5 | @ | @ | @ | @ | ||
| 6 | @ | @ | @ | @ | @ | |
| 7 | @ | @ | @ | @ | @ | @ |








Last revised 2023-10-15.