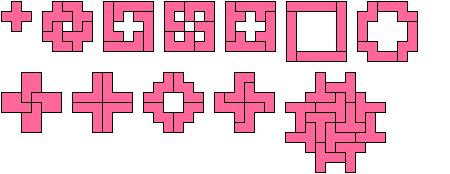Baiocchi Figures for Polyominoes
A Baiocchi figure is a figure
formed by joining copies of a polyform and having the maximal
symmetry for the polyform's class.
For polyominoes, that means square symmetry, or 4-way rotary with reflection.
If a polyomino lacks diagonal symmetry, its Baiocchi figures
must be Galvagni figures or contain Galvagni figures.
Claudio
Baiocchi proposed the idea in January 2008.
Baiocchi figures first appeared in Erich Friedman's
Math Magic for that month.
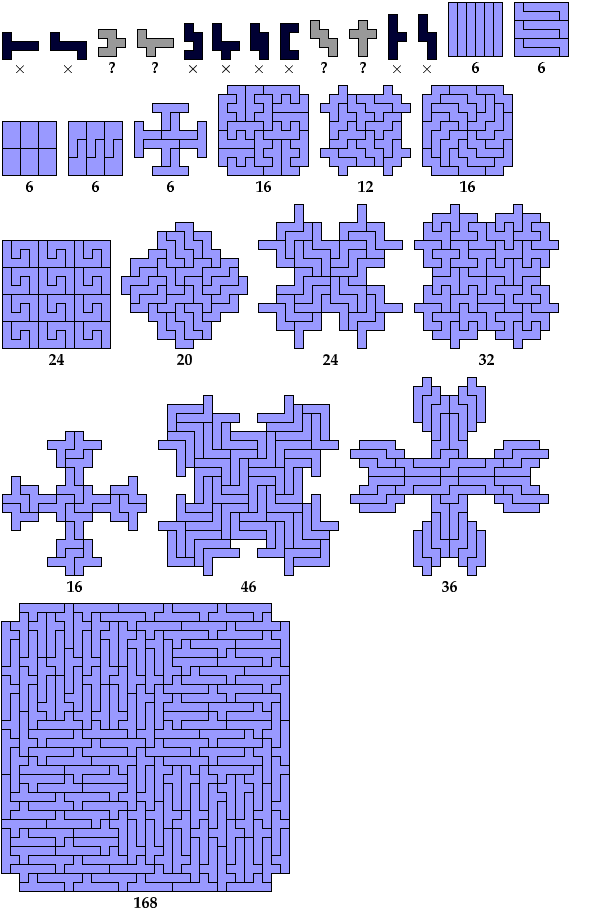
Here are minimal known Baiocchi figures for polyominoes
of orders 1 through 8.
Dr. Friedman found most of the smaller figures up to order 6,
and Corey Plover discovered the 12-tile hexomino figure
while investigating Galvagni figures.
Not all these solutions are uniquely minimal.
A one-sided solution is one in which the polyomino is not reflected.




Holeless Variants
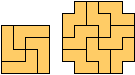
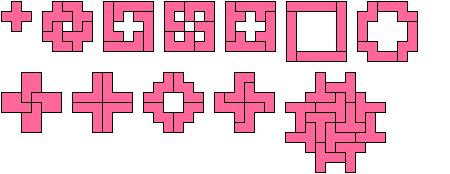
Holeless Variants
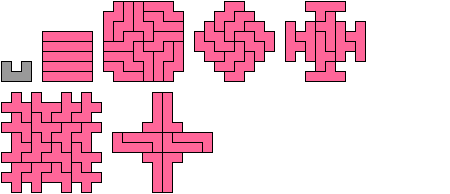
Variant with Minimal Hole Area
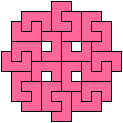
One-Sided Holeless Variants
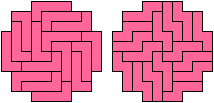

One-Sided Variants
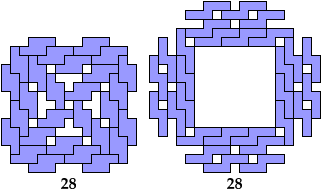
Holeless Variants
Variants with Minimal Hole Area

One-Sided Holeless Variants
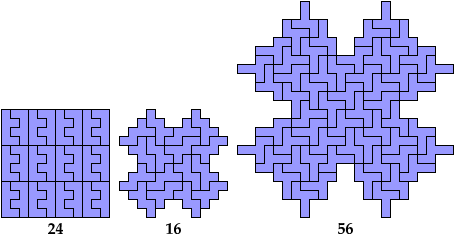

Holeless Variants
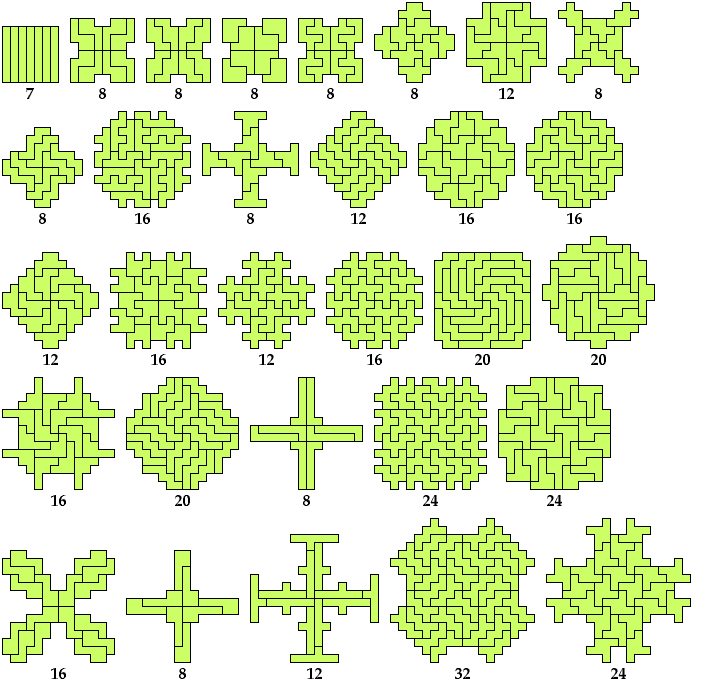

Holeless Variants
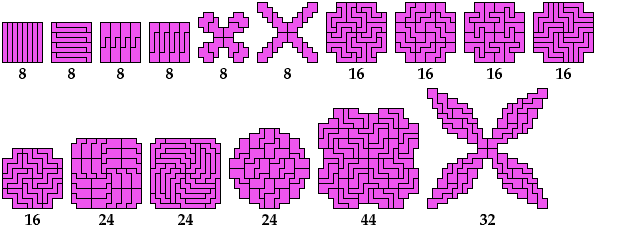
Last revised 2023-09-28.
Back to Baiocchi Figures
<
Polyform Compatibility
<
Polyform Curiosities
George Sicherman
[ HOME
| MAIL
]