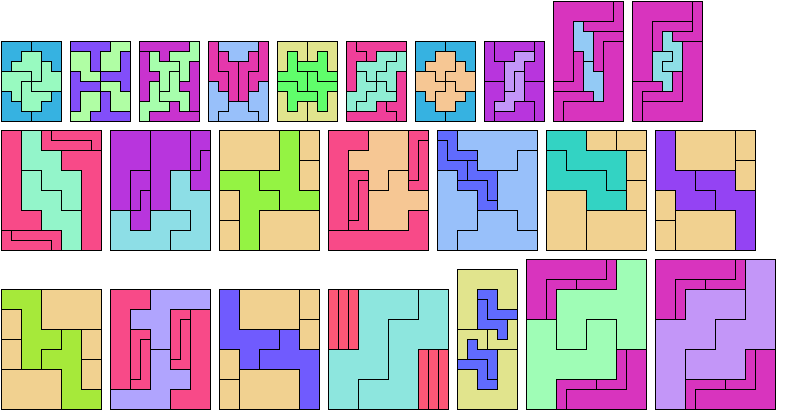
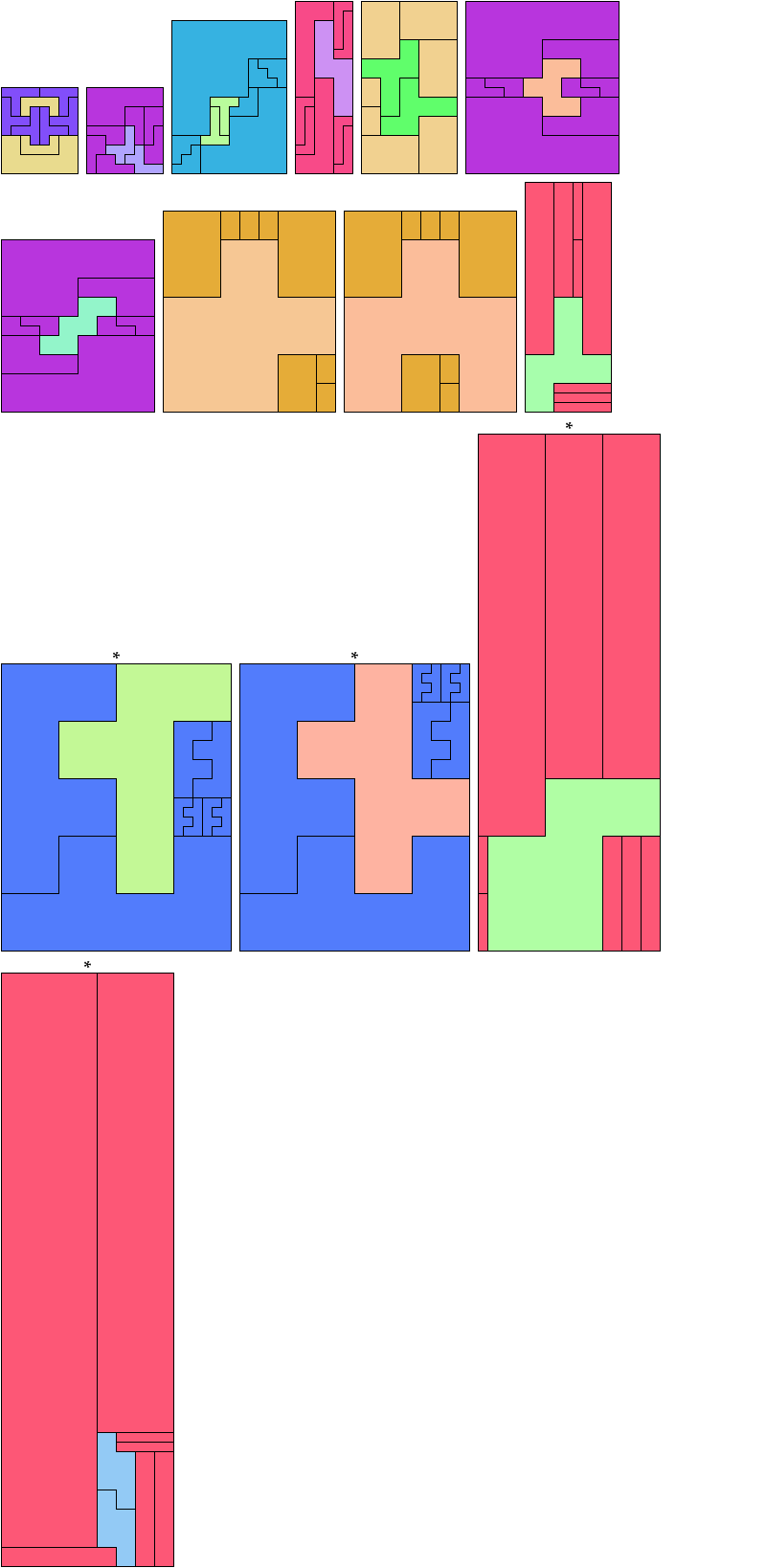
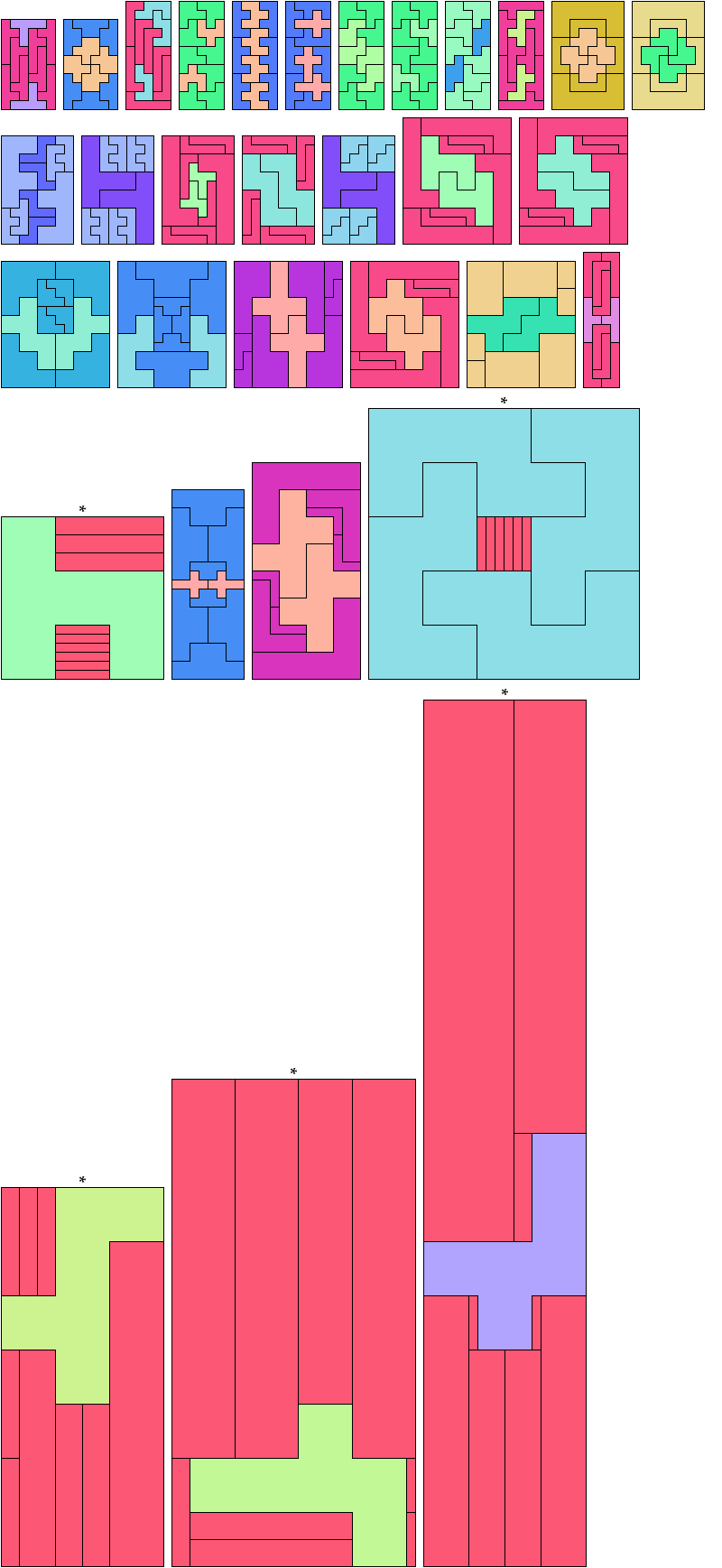
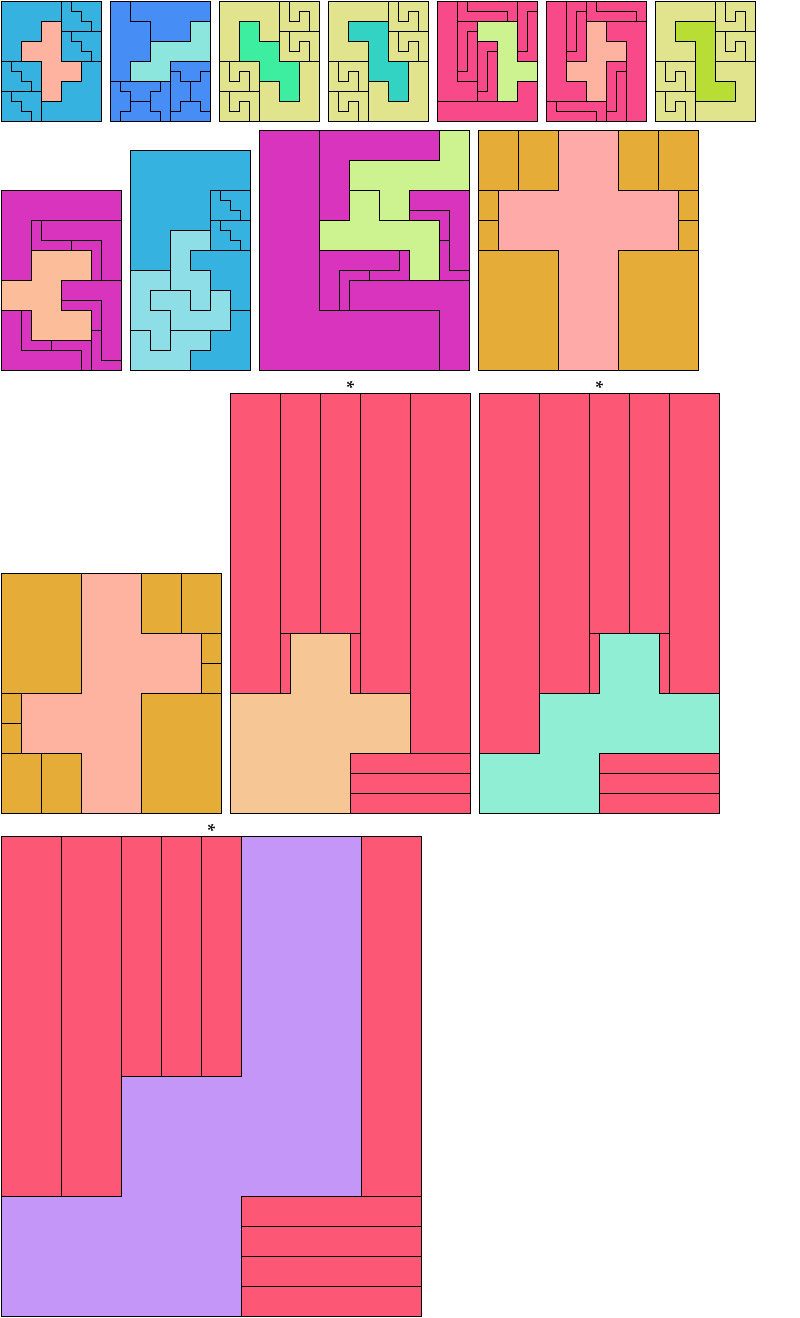
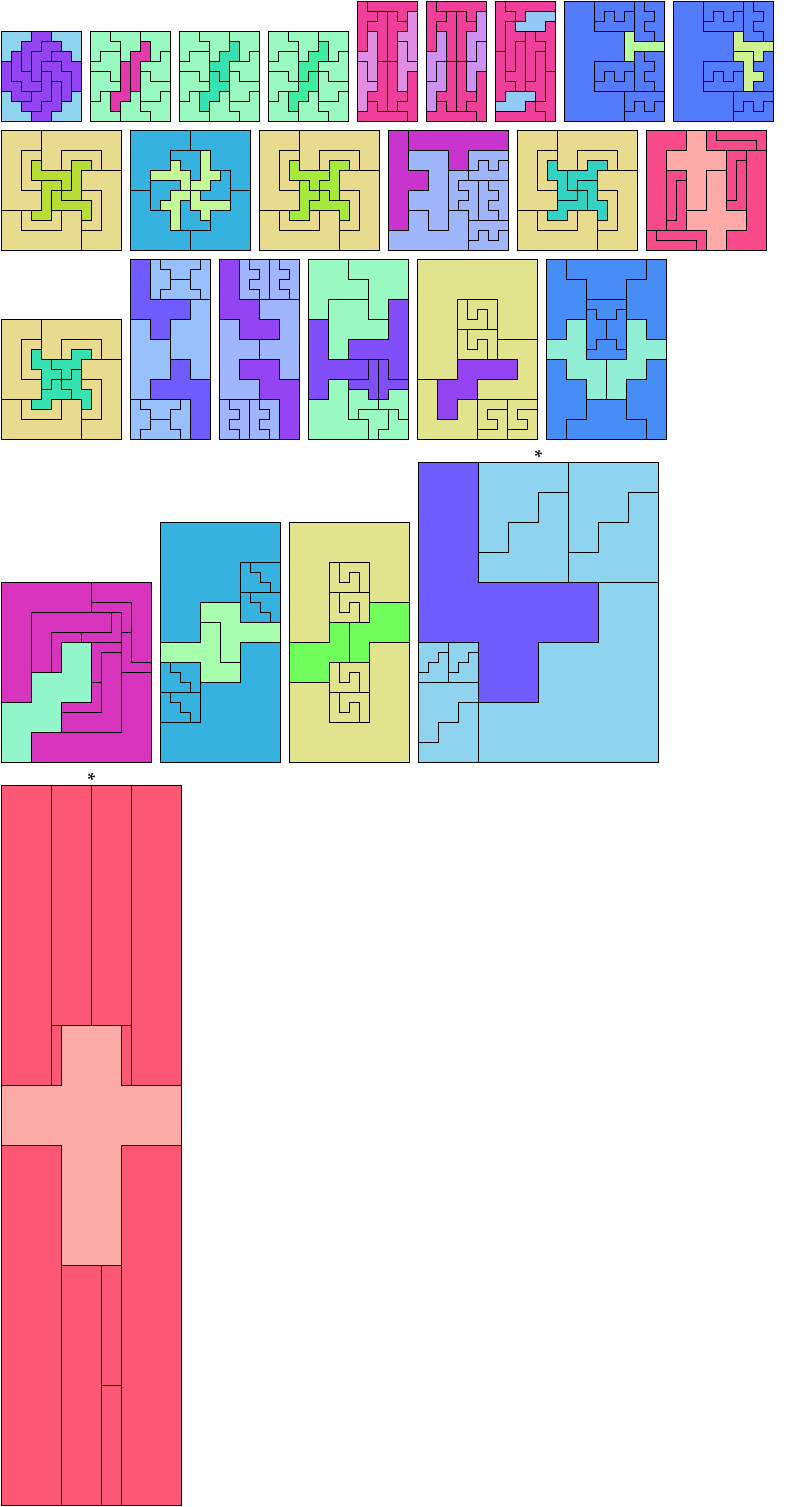
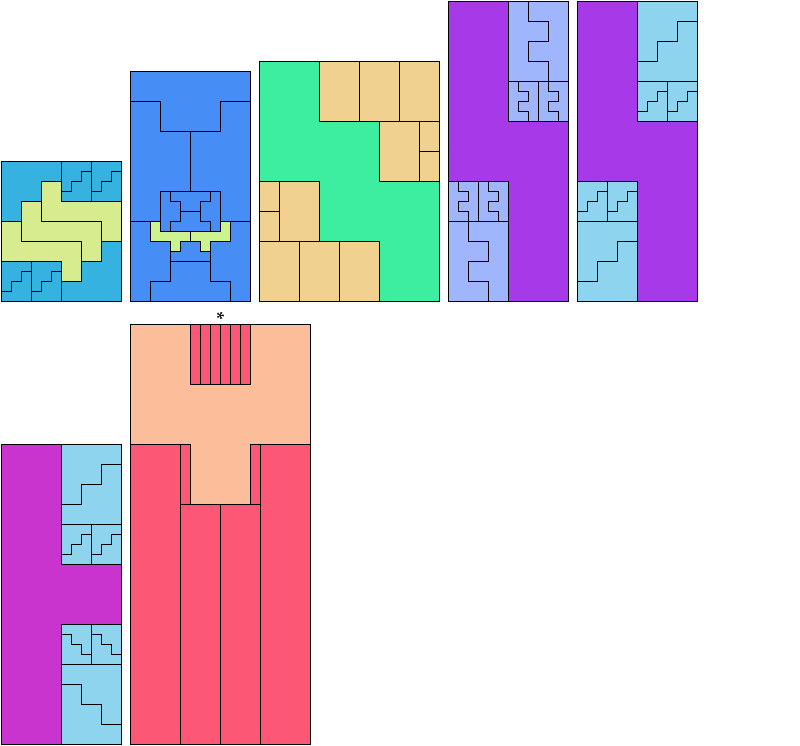
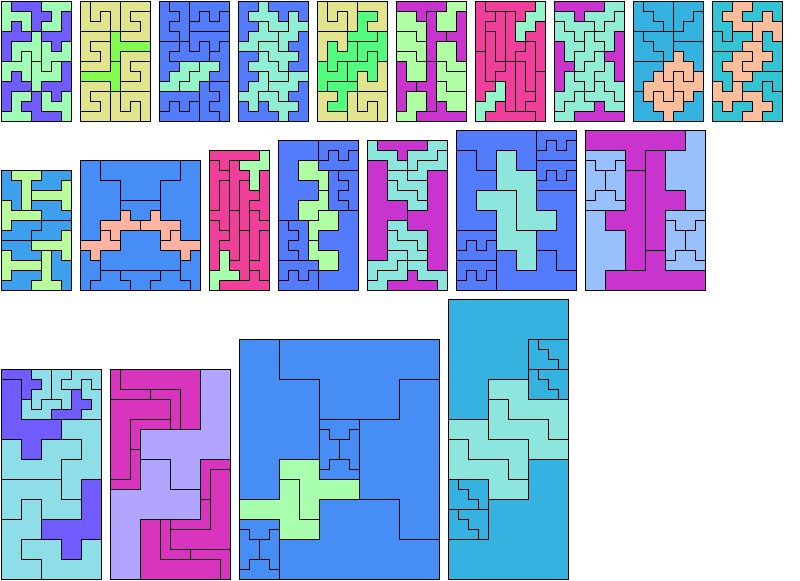
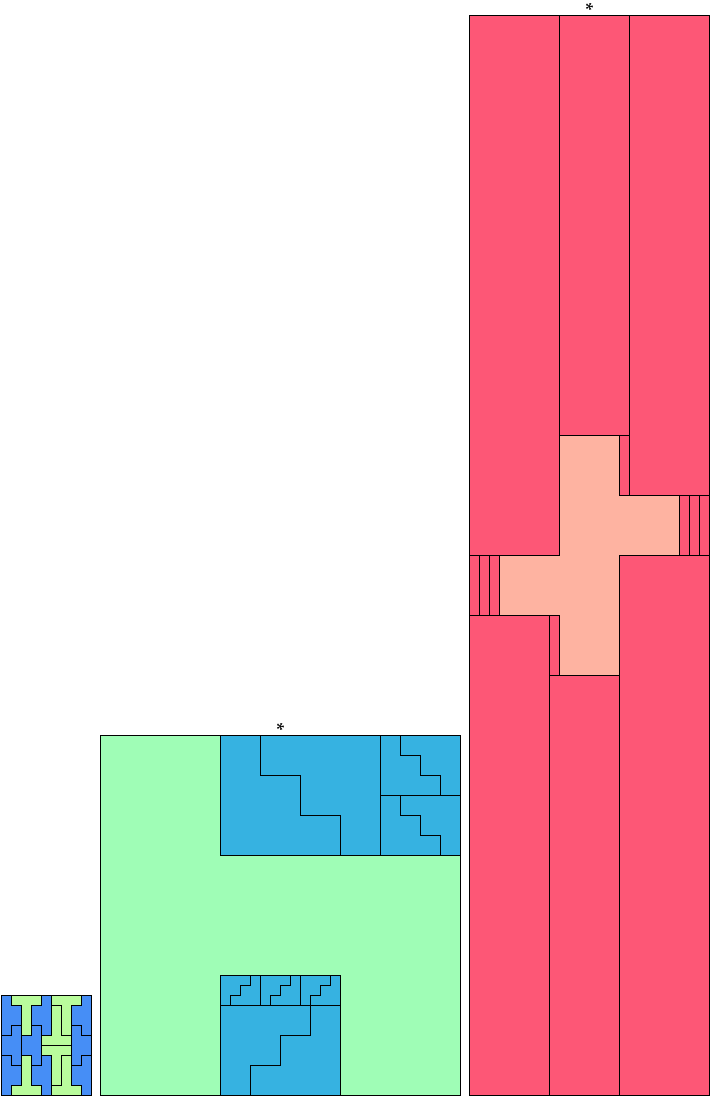
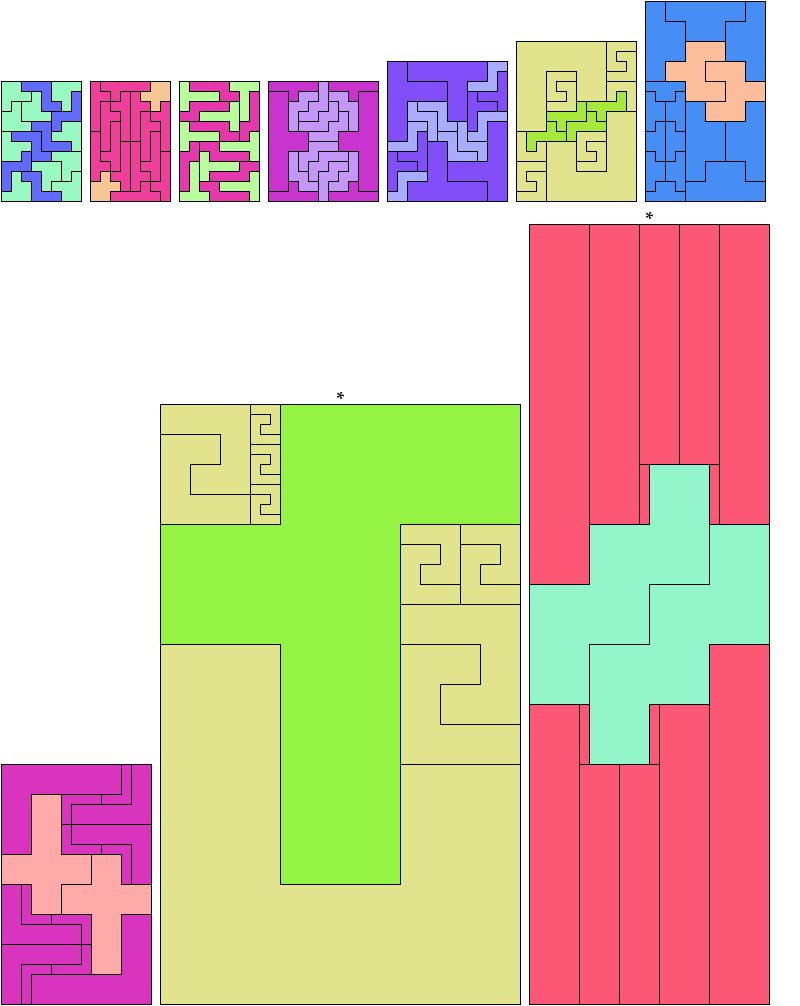
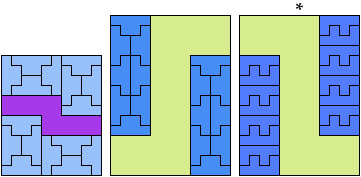
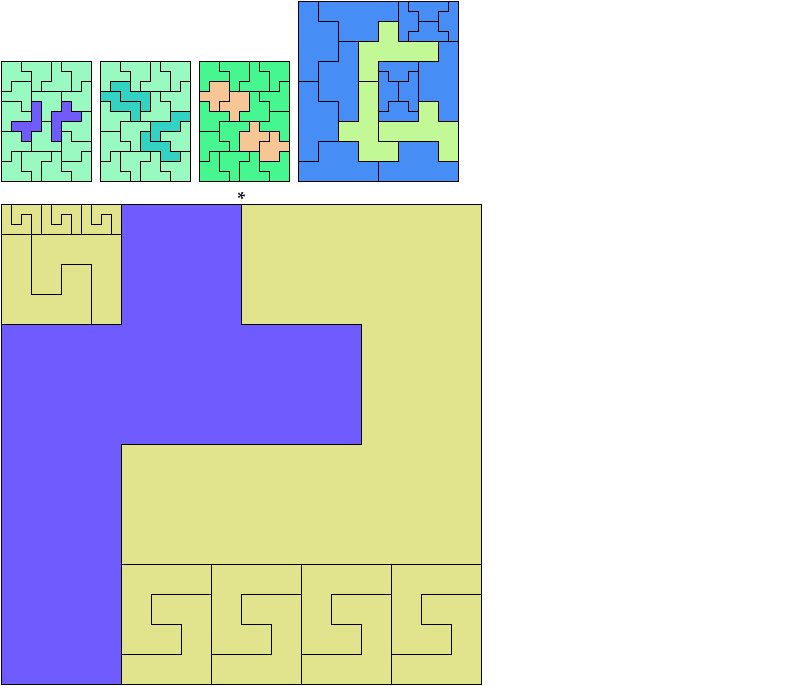
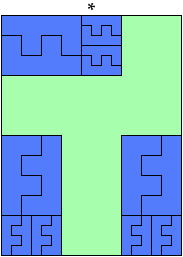
If you find a solution with fewer tiles or solve an unsolved case, please write.
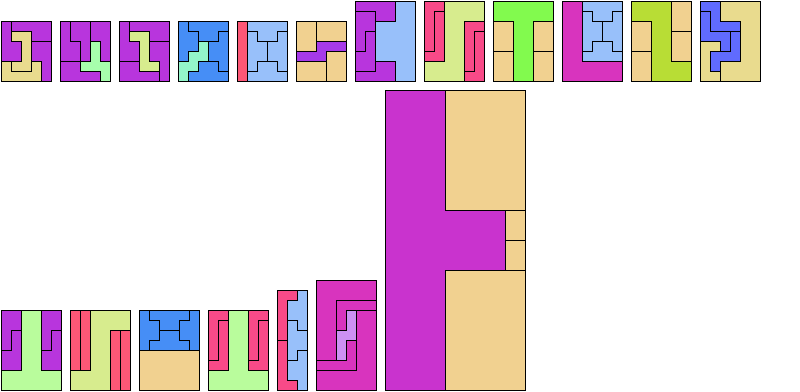
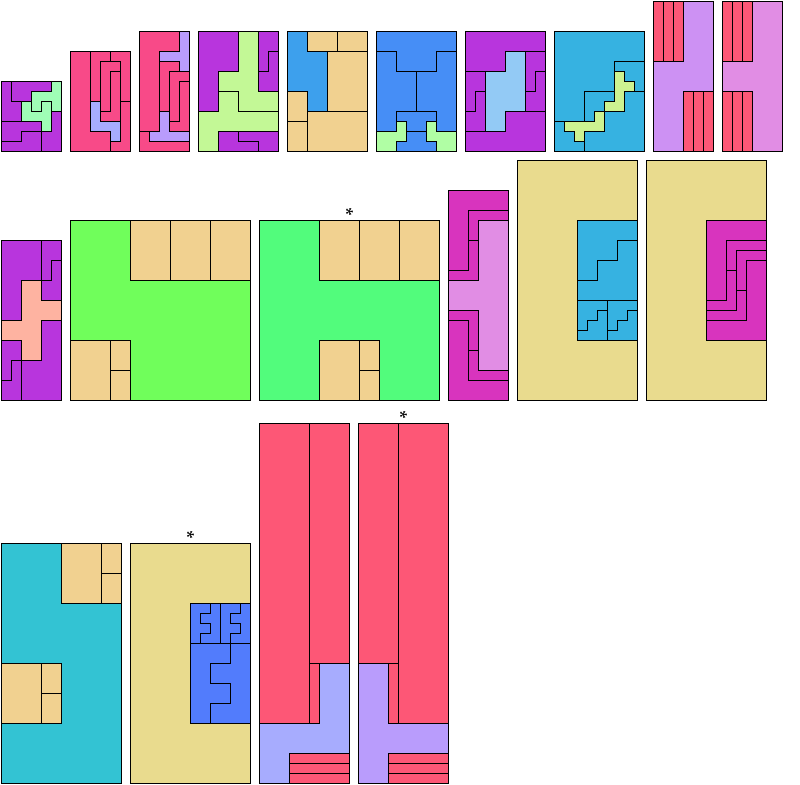
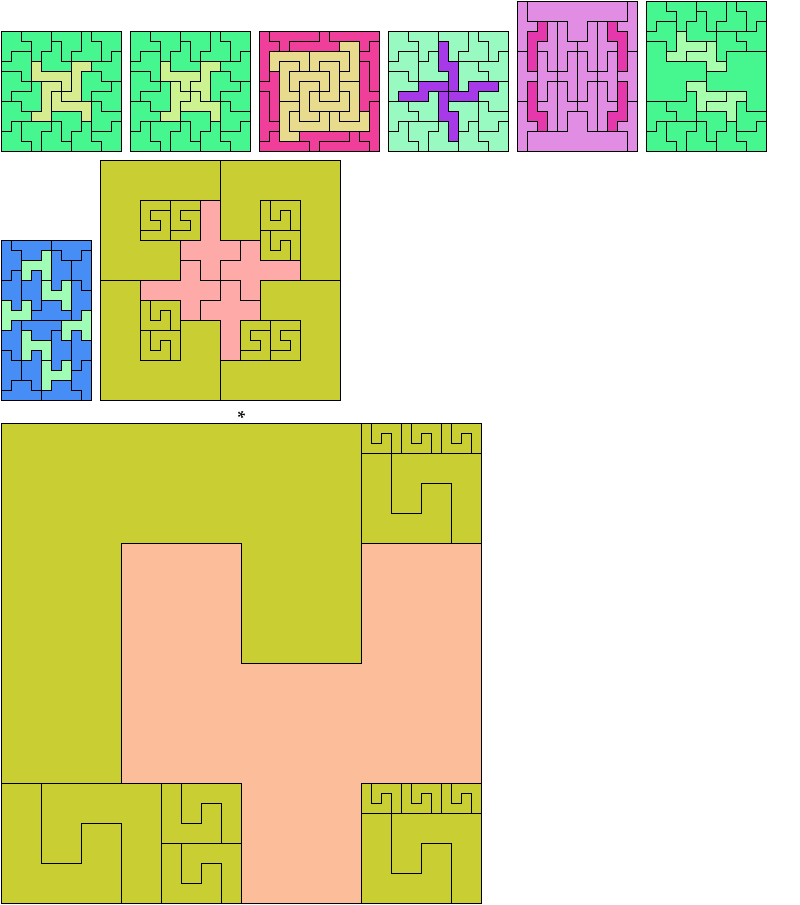
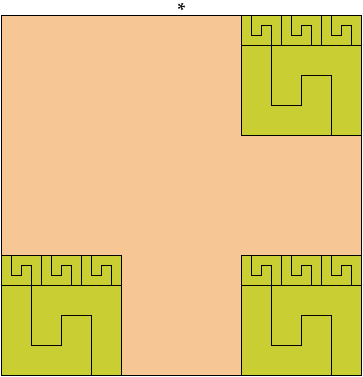
Carl Schwenke and Johann Schwenke found the tilings marked with an asterisk (*).
See also Hexomino Pair Rectangles.
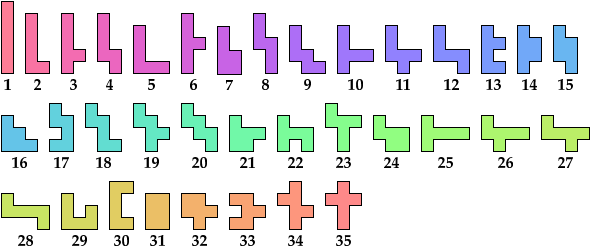
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | • | 3 | 6 | 6 | 4 | 7 | 3 | 7 | 11 | 7 | 10 | 7 | 3 | 5 | 9 | 3 | 10 | 8 | 11 | 16 | 6 | 10 | 9 | 9 | 4 | 10 | 10 | 5 | 3 | 4 | 2 | 11 | 13 | 15 | 12 |
| 2 | 3 | • | 4 | 4 | 4 | 10 | 4 | 9 | 4 | 7 | 8 | 7 | 4 | 5 | 4 | 4 | 10 | 10 | 10 | 8 | 6 | 10 | 10 | 4 | 5 | 4 | 11 | 5 | 4 | 6 | 3 | 8 | 10 | 11 | 12 |
| 3 | 6 | 4 | • | 21 | 6 | 12 | 6 | 12 | 20 | 10 | 20 | 6 | 6 | 6 | 12 | 4 | 4 | 6 | 8 | 14 | 4 | 4 | 14 | 6 | 4 | 20 | 10 | 30 | 6 | 24 | 4 | 16 | 44 | 96 | 64 |
| 4 | 6 | 4 | 21 | • | 4 | 24 | 6 | × | × | 42 | × | × | 6 | 8 | × | 4 | 6 | × | × | × | 12 | 30 | × | × | 16 | × | × | × | 4 | 6 | 6 | × | ? | × | × |
| 5 | 4 | 4 | 6 | 4 | • | 7 | 3 | 5 | 8 | 6 | 14 | 4 | 4 | 5 | 8 | 4 | 8 | 4 | 6 | 12 | 4 | 8 | 4 | 4 | 6 | 6 | 11 | 3 | 4 | 7 | 2 | 6 | 11 | 10 | 16 |
| 6 | 7 | 10 | 12 | 24 | 7 | • | 3 | ? | 16 | 50 | ? | 21 | 12 | 14 | 94 | 13 | 6 | 14 | 14 | ? | 4 | 52 | 8 | 14 | ? | 96 | ? | ? | 6 | ? | 5 | 164 | 96 | ? | ? |
| 7 | 3 | 4 | 6 | 6 | 3 | 3 | • | 3 | 8 | 3 | 9 | 4 | 4 | 5 | 7 | 4 | 8 | 4 | 6 | 9 | 4 | 7 | 5 | 4 | 5 | 7 | 6 | 5 | 4 | 5 | 3 | 6 | 9 | 7 | 10 |
| 8 | 7 | 9 | 12 | × | 5 | ? | 3 | • | × | 400 | × | × | 13 | 17 | × | 13 | ? | × | × | × | 24 | ? | × | × | ? | × | × | × | 4 | ? | 5 | × | ? | × | × |
| 9 | 11 | 4 | 20 | × | 8 | 16 | 8 | × | • | 22 | × | × | 12 | 6 | × | 12 | ? | × | × | × | 6 | ? | × | × | ? | × | × | × | 12 | 32 | 8 | × | ? | × | × |
| 10 | 7 | 7 | 10 | 42 | 6 | 50 | 3 | 400 | 22 | • | ? | 16 | 10 | 4 | 44 | 10 | 102 | 6 | ? | ? | 12 | 50 | ? | 8 | ? | ? | 96 | ? | 6 | 9 | 4 | 80 | ? | ? | ? |
| 11 | 10 | 8 | 20 | × | 14 | ? | 9 | × | × | ? | • | × | 4 | 12 | × | 12 | 14 | × | × | × | 18 | 14 | × | × | ? | × | × | × | 18 | ? | 8 | × | ? | × | × |
| 12 | 7 | 7 | 6 | × | 4 | 21 | 4 | × | × | 16 | × | • | 10 | 8 | × | 6 | 32 | × | × | × | 16 | 106 | × | × | ? | × | × | × | 8 | 5 | 6 | × | ? | × | × |
| 13 | 3 | 4 | 6 | 6 | 4 | 12 | 4 | 13 | 12 | 10 | 4 | 10 | • | 4 | 4 | 4 | 6 | 14 | 14 | 14 | 6 | 4 | 19 | 14 | 12 | 9 | 12 | 17 | 4 | 7 | 3 | 4 | 10 | 9 | 10 |
| 14 | 5 | 5 | 6 | 8 | 5 | 14 | 5 | 17 | 6 | 4 | 12 | 8 | 4 | • | 6 | 3 | 10 | 11 | 12 | 5 | 4 | 24 | 14 | 7 | 15 | 18 | 13 | 17 | 3 | 2 | 5 | 10 | 16 | 14 | 10 |
| 15 | 9 | 4 | 12 | × | 8 | 94 | 7 | × | × | 44 | × | × | 4 | 6 | • | 4 | ? | × | × | × | 10 | 48 | × | × | 14 | × | × | × | 4 | ? | 7 | × | ? | × | × |
| 16 | 3 | 4 | 4 | 4 | 4 | 13 | 4 | 13 | 12 | 10 | 12 | 6 | 4 | 3 | 4 | • | 11 | 14 | 10 | 3 | 8 | 15 | 12 | 6 | 9 | 12 | 7 | 13 | 4 | 7 | 3 | 8 | 14 | 11 | 20 |
| 17 | 10 | 10 | 4 | 6 | 8 | 6 | 8 | ? | ? | 102 | 14 | 32 | 6 | 10 | ? | 11 | • | 120 | 100 | ? | 4 | ? | ? | ? | ? | 64 | 168 | ? | 3 | 6 | 7 | 54 | 14 | ? | ? |
| 18 | 8 | 10 | 6 | × | 4 | 14 | 4 | × | × | 6 | × | × | 14 | 11 | × | 14 | 120 | • | × | × | 18 | ? | × | × | ? | × | × | × | 11 | 12 | 8 | × | ? | × | × |
| 19 | 11 | 10 | 8 | × | 6 | 14 | 6 | × | × | ? | × | × | 14 | 12 | × | 10 | 100 | × | • | × | 12 | ? | × | × | ? | × | × | × | 4 | 12 | 10 | × | ? | × | × |
| 20 | 16 | 8 | 14 | × | 12 | ? | 9 | × | × | ? | × | × | 14 | 5 | × | 3 | ? | × | × | • | 12 | ? | × | × | ? | × | × | × | 11 | ? | 13 | × | ? | × | × |
| 21 | 6 | 6 | 4 | 12 | 4 | 4 | 4 | 24 | 6 | 12 | 18 | 16 | 6 | 4 | 10 | 8 | 4 | 18 | 12 | 12 | • | 10 | 24 | 10 | 28 | 22 | 24 | 24 | 2 | 10 | 6 | 18 | 10 | 28 | 36 |
| 22 | 10 | 10 | 4 | 30 | 8 | 52 | 7 | ? | ? | 50 | 14 | 106 | 4 | 24 | 48 | 15 | ? | ? | ? | ? | 10 | • | ? | ? | ? | ? | ? | ? | 14 | 112 | 7 | 28 | ? | ? | ? |
| 23 | 9 | 10 | 14 | × | 4 | 8 | 5 | × | × | ? | × | × | 19 | 14 | × | 12 | ? | × | × | × | 24 | ? | • | × | ? | × | × | × | 8 | 70 | 9 | × | ? | × | × |
| 24 | 9 | 4 | 6 | × | 4 | 14 | 4 | × | × | 8 | × | × | 14 | 7 | × | 6 | ? | × | × | × | 10 | ? | × | • | 22 | × | × | × | 12 | 4 | 7 | × | ? | × | × |
| 25 | 4 | 5 | 4 | 16 | 6 | ? | 5 | ? | ? | ? | ? | ? | 12 | 15 | 14 | 9 | ? | ? | ? | ? | 28 | ? | ? | 22 | • | ? | ? | ? | 14 | 6 | 5 | ? | ? | ? | ? |
| 26 | 10 | 4 | 20 | × | 6 | 96 | 7 | × | × | ? | × | × | 9 | 18 | × | 12 | 64 | × | × | × | 22 | ? | × | × | ? | • | × | × | 16 | 22 | 8 | × | ? | × | × |
| 27 | 10 | 11 | 10 | × | 11 | ? | 6 | × | × | 96 | × | × | 12 | 13 | × | 7 | 168 | × | × | × | 24 | ? | × | × | ? | × | • | × | 16 | 12 | 8 | × | ? | × | × |
| 28 | 5 | 5 | 30 | × | 3 | ? | 5 | × | × | ? | × | × | 17 | 17 | × | 13 | ? | × | × | × | 24 | ? | × | × | ? | × | × | • | 11 | 12 | 5 | × | ? | × | × |
| 29 | 3 | 4 | 6 | 4 | 4 | 6 | 4 | 4 | 12 | 6 | 18 | 8 | 4 | 3 | 4 | 4 | 3 | 11 | 4 | 11 | 2 | 14 | 8 | 12 | 14 | 16 | 16 | 11 | • | 3 | 3 | 25 | 24 | 3 | 24 |
| 30 | 4 | 6 | 24 | 6 | 7 | ? | 5 | ? | 32 | 9 | ? | 5 | 7 | 2 | ? | 7 | 6 | 12 | 12 | ? | 10 | 112 | 70 | 4 | 6 | 22 | 12 | 12 | 3 | • | 4 | 10 | ? | ? | ? |
| 31 | 2 | 3 | 4 | 6 | 2 | 5 | 3 | 5 | 8 | 4 | 8 | 6 | 3 | 5 | 7 | 3 | 7 | 8 | 10 | 13 | 6 | 7 | 9 | 7 | 5 | 8 | 8 | 5 | 3 | 4 | • | 9 | 9 | 11 | 11 |
| 32 | 11 | 8 | 16 | × | 6 | 164 | 6 | × | × | 80 | × | × | 4 | 10 | × | 8 | 54 | × | × | × | 18 | 28 | × | × | ? | × | × | × | 25 | 10 | 9 | • | ? | × | × |
| 33 | 13 | 10 | 44 | ? | 11 | 96 | 9 | ? | ? | ? | ? | ? | 10 | 16 | ? | 14 | 14 | ? | ? | ? | 10 | ? | ? | ? | ? | ? | ? | ? | 24 | ? | 9 | ? | • | ? | ? |
| 34 | 15 | 11 | 96 | × | 10 | ? | 7 | × | × | ? | × | × | 9 | 14 | × | 11 | ? | × | × | × | 28 | ? | × | × | ? | × | × | × | 3 | ? | 11 | × | ? | • | × |
| 35 | 12 | 12 | 64 | × | 16 | ? | 10 | × | × | ? | × | × | 10 | 10 | × | 20 | ? | × | × | × | 36 | ? | × | × | ? | × | × | × | 24 | ? | 11 | × | ? | × | • |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |














 Last revised 2024-03-26.
Last revised 2024-03-26.