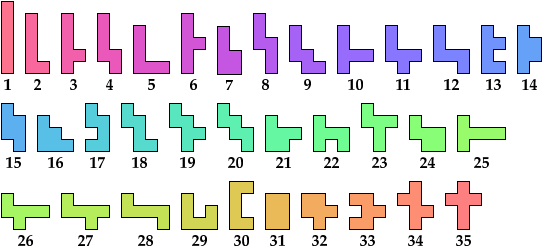
The problem of arranging copies of a polyomino to form a rectangle has been studied for a long time. Here I study the problem of arranging copies of two hexominoes to form a rectangle with one corner cell removed.
If you find a smaller solution or solve an unsolved case, please write.
See also

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | * | 8 | 8 | 8 | 8 | 15 | 8 | 15 | 28 | 15 | 41 | 15 | 8 | 8 | 8 | 8 | 41 | 15 | 41 | 28 | 15 | 28 | ? | 8 | 15 | 28 | 129 | 36 | 8 | 28 | 8 | 559 | 28 | ? | ? |
| 2 | 8 | * | 8 | 8 | 8 | 8 | 8 | 20 | 8 | 15 | 20 | 14 | 8 | 8 | 8 | 8 | 9 | 15 | 28 | 28 | 8 | 22 | 22 | 8 | 20 | 8 | 22 | 15 | 8 | 15 | 8 | 28 | 15 | 15 | 22 |
| 3 | 8 | 8 | * | 29 | 20 | ? | 8 | 41 | 15 | 67 | 42 | 8 | 8 | 15 | 28 | 8 | 19 | 41 | 48 | 22 | 8 | 28 | 54 | 14 | 28 | 28 | 64 | 54 | 22 | ? | 8 | 82 | 86 | ? | ? |
| 4 | 8 | 8 | 29 | * | 15 | 64 | 8 | ? | ? | 80 | ? | ? | 9 | 28 | ? | 9 | 41 | ? | ? | ? | 20 | 31 | ? | ? | 41 | ? | ? | ? | 8 | ? | 4 | ? | ? | ? | ? |
| 5 | 8 | 8 | 20 | 15 | * | 54 | 4 | ? | 29 | ? | ? | 9 | 15 | 22 | ? | 8 | 67 | 15 | 28 | ? | 4 | 67 | 22 | 15 | 28 | 41 | 42 | 8 | 4 | 14 | 8 | 60 | ? | ? | ? |
| 6 | 15 | 8 | ? | 64 | 54 | * | 9 | ? | ? | ? | ? | 48 | 41 | 48 | ? | ? | 41 | 54 | 54 | ? | 14 | ? | ? | 20 | ? | ? | ? | ? | 48 | ? | 28 | ? | ? | ? | ? |
| 7 | 8 | 8 | 8 | 8 | 4 | 9 | * | 8 | 8 | 4 | 14 | 8 | 8 | 8 | 15 | 9 | 20 | 4 | 15 | 28 | 4 | 15 | 4 | 4 | 15 | 8 | 15 | 14 | 9 | 8 | 4 | 8 | 28 | 15 | 15 |
| 8 | 15 | 20 | 41 | ? | ? | ? | 8 | * | ? | ? | ? | ? | ? | 54 | ? | ? | ? | ? | ? | ? | 54 | ? | ? | ? | ? | ? | ? | ? | 28 | ? | ? | ? | ? | ? | ? |
| 9 | 28 | 8 | 15 | ? | 29 | ? | 8 | ? | * | 53 | ? | ? | 20 | 8 | ? | 8 | ? | ? | ? | ? | 8 | ? | ? | ? | ? | ? | ? | ? | 28 | ? | 41 | ? | ? | ? | ? |
| 10 | 15 | 15 | 67 | 80 | ? | ? | 4 | ? | 53 | * | ? | ? | 15 | 28 | ? | 54 | ? | 31 | ? | ? | 15 | ? | ? | 8 | ? | ? | ? | ? | 4 | ? | 8 | 82 | ? | ? | ? |
| 11 | 41 | 20 | 42 | ? | ? | ? | 14 | ? | ? | ? | * | ? | 48 | 48 | ? | 28 | ? | ? | ? | ? | 19 | 54 | ? | ? | ? | ? | ? | ? | 8 | ? | ? | ? | ? | ? | ? |
| 12 | 15 | 14 | 8 | ? | 9 | 48 | 8 | ? | ? | ? | ? | * | 31 | 48 | ? | ? | ? | ? | ? | ? | 22 | ? | ? | ? | ? | ? | ? | ? | 41 | 28 | 8 | ? | ? | ? | ? |
| 13 | 8 | 8 | 8 | 9 | 15 | 41 | 8 | ? | 20 | 15 | 48 | 31 | * | 15 | 20 | 82 | 15 | 31 | 42 | 28 | 8 | 8 | 41 | 31 | 48 | 20 | 48 | ? | 41 | 54 | 20 | 8 | 15 | 41 | 4 |
| 14 | 8 | 8 | 15 | 28 | 22 | 48 | 8 | 54 | 8 | 28 | 48 | 48 | 15 | * | 28 | 8 | 28 | 41 | 28 | 8 | 4 | 48 | ? | 14 | 67 | 20 | 48 | 54 | 14 | 28 | 20 | 19 | 28 | 41 | ? |
| 15 | 8 | 8 | 28 | ? | ? | ? | 15 | ? | ? | ? | ? | ? | 20 | 28 | * | 20 | ? | ? | ? | ? | 20 | 48 | ? | ? | 8 | ? | ? | ? | 9 | ? | 8 | ? | ? | ? | ? |
| 16 | 8 | 8 | 8 | 9 | 8 | ? | 9 | ? | 8 | 54 | 28 | ? | 82 | 8 | 20 | * | 80 | ? | 28 | 8 | 8 | ? | ? | 20 | ? | ? | ? | ? | 8 | ? | 8 | 4 | 54 | ? | ? |
| 17 | 41 | 9 | 19 | 41 | 67 | 41 | 20 | ? | ? | ? | ? | ? | 15 | 28 | ? | 80 | * | ? | ? | ? | 20 | ? | ? | ? | ? | 79 | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| 18 | 15 | 15 | 41 | ? | 15 | 54 | 4 | ? | ? | 31 | ? | ? | 31 | 41 | ? | ? | ? | * | ? | ? | 28 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 28 | ? | ? | ? | ? |
| 19 | 41 | 28 | 48 | ? | 28 | 54 | 15 | ? | ? | ? | ? | ? | 42 | 28 | ? | 28 | ? | ? | * | ? | 41 | ? | ? | ? | ? | ? | ? | ? | 22 | ? | ? | ? | ? | ? | ? |
| 20 | 28 | 28 | 22 | ? | ? | ? | 28 | ? | ? | ? | ? | ? | 28 | 8 | ? | 8 | ? | ? | ? | * | 48 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| 21 | 15 | 8 | 8 | 20 | 4 | 14 | 4 | 54 | 8 | 15 | 19 | 22 | 8 | 4 | 20 | 8 | 20 | 28 | 41 | 48 | * | 41 | 42 | 4 | 48 | 28 | 41 | 48 | 28 | 31 | 4 | 28 | 4 | 48 | 41 |
| 22 | 28 | 22 | 28 | 31 | 67 | ? | 15 | ? | ? | ? | 54 | ? | 8 | 48 | 48 | ? | ? | ? | ? | ? | 41 | * | ? | ? | ? | ? | ? | ? | 8 | ? | ? | 48 | ? | ? | ? |
| 23 | ? | 22 | 54 | ? | 22 | ? | 4 | ? | ? | ? | ? | ? | 41 | ? | ? | ? | ? | ? | ? | ? | 42 | ? | * | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| 24 | 8 | 8 | 14 | ? | 15 | 20 | 4 | ? | ? | 8 | ? | ? | 31 | 14 | ? | 20 | ? | ? | ? | ? | 4 | ? | ? | * | 41 | ? | ? | ? | ? | ? | 4 | ? | ? | ? | ? |
| 25 | 15 | 20 | 28 | 41 | 28 | ? | 15 | ? | ? | ? | ? | ? | 48 | 67 | 8 | ? | ? | ? | ? | ? | 48 | ? | ? | 41 | * | ? | ? | ? | ? | ? | 8 | ? | ? | ? | ? |
| 26 | 28 | 8 | 28 | ? | 41 | ? | 8 | ? | ? | ? | ? | ? | 20 | 20 | ? | ? | 79 | ? | ? | ? | 28 | ? | ? | ? | ? | * | ? | ? | 28 | ? | ? | ? | ? | ? | ? |
| 27 | 129 | 22 | 64 | ? | 42 | ? | 15 | ? | ? | ? | ? | ? | 48 | 48 | ? | ? | ? | ? | ? | ? | 41 | ? | ? | ? | ? | ? | * | ? | ? | ? | 28 | ? | ? | ? | ? |
| 28 | 36 | 15 | 54 | ? | 8 | ? | 14 | ? | ? | ? | ? | ? | ? | 54 | ? | ? | ? | ? | ? | ? | 48 | ? | ? | ? | ? | ? | ? | * | ? | ? | 8 | ? | ? | ? | ? |
| 29 | 8 | 8 | 22 | 8 | 4 | 48 | 9 | 28 | 28 | 4 | 8 | 41 | 41 | 14 | 9 | 8 | ? | ? | 22 | ? | 28 | 8 | ? | ? | ? | 28 | ? | ? | * | ? | ? | ? | ? | ? | ? |
| 30 | 28 | 15 | ? | ? | 14 | ? | 8 | ? | ? | ? | ? | 28 | 54 | 28 | ? | ? | ? | ? | ? | ? | 31 | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? | ? | ? |
| 31 | 8 | 8 | 8 | 4 | 8 | 28 | 4 | ? | 41 | 8 | ? | 8 | 20 | 20 | 8 | 8 | ? | 28 | ? | ? | 4 | ? | ? | 4 | 8 | ? | 28 | 8 | ? | ? | * | ? | ? | ? | ? |
| 32 | 559 | 28 | 82 | ? | 60 | ? | 8 | ? | ? | 82 | ? | ? | 8 | 19 | ? | 4 | ? | ? | ? | ? | 28 | 48 | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? | ? |
| 33 | 28 | 15 | 86 | ? | ? | ? | 28 | ? | ? | ? | ? | ? | 15 | 28 | ? | 54 | ? | ? | ? | ? | 4 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? | ? |
| 34 | ? | 15 | ? | ? | ? | ? | 15 | ? | ? | ? | ? | ? | 41 | 41 | ? | ? | ? | ? | ? | ? | 48 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * | ? |
| 35 | ? | 22 | ? | ? | ? | ? | 15 | ? | ? | ? | ? | ? | 4 | ? | ? | ? | ? | ? | ? | ? | 41 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | * |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |



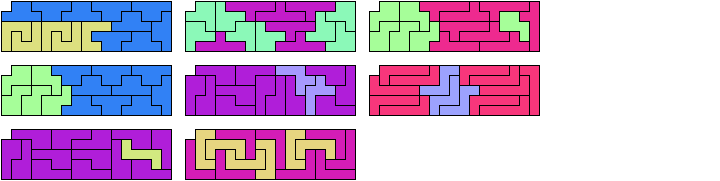



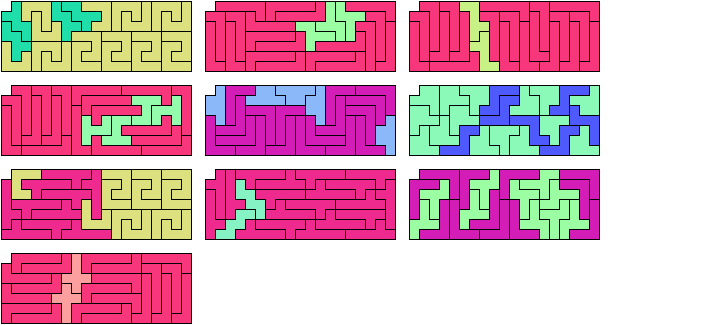


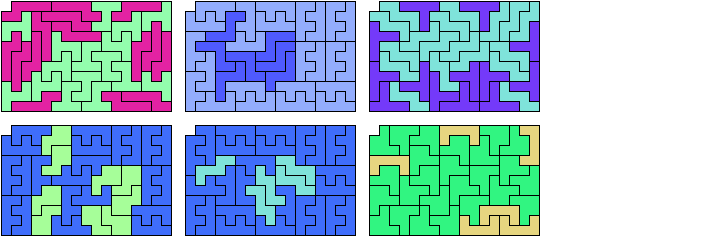










Last revised 2023-06-23.