Scaled Three-Pentomino Rectangles

Introduction

A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

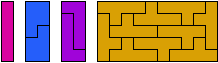
It has long been known that only four pentominoes can tile rectangles:

For other rectangles that these pentominoes tile, see Mike Reid's Rectifiable Polyomino Page.

On Scaled Two-Pentomino Rectangles I study the related problem of tiling some rectangle with two pentominoes at various sizes. Here I study the corresponding problem for three pentominoes in various sizes. If you find a solution with fewer tiles than one of mine, please write!

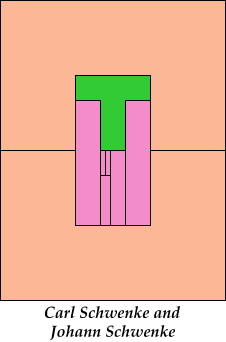
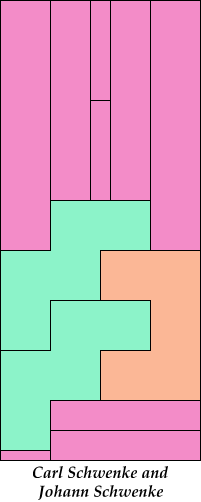
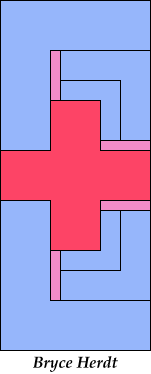
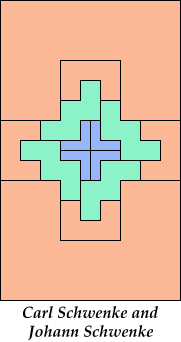
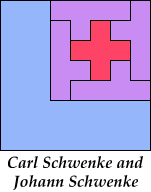
Bryce Herdt has already improved on one of my solutions.

See also Scaled Three-Pentomino Balanced Rectangles.

Nomenclature

I use Solomon W. Golomb's original names for the pentominoes:

Solutions

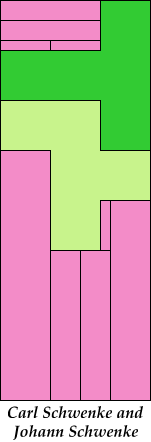
5F+5I+5L 55F+5I+5N 125F+5I+5P 65F+5I+5T 145F+5I+5U 6
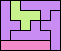
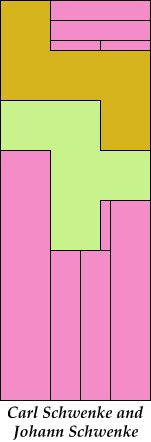
5F+5I+5V 55F+5I+5W 145F+5I+5X 175F+5I+5Y 65F+5I+5Z 14
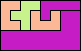
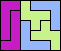
5F+5L+5N 65F+5L+5P 45F+5L+5T 65F+5L+5U 55F+5L+5V 6
5F+5L+5W 65F+5L+5X 95F+5L+5Y 55F+5L+5Z 75F+5N+5P 6
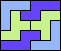
5F+5N+5T 115F+5N+5U 65F+5N+5V 65F+5N+5W ×5F+5N+5X ×
5F+5N+5Y 75F+5N+5Z ×5F+5P+5T 65F+5P+5U 35F+5P+5V 4
5F+5P+5W 85F+5P+5X 95F+5P+5Y 55F+5P+5Z 65F+5T+5U 9
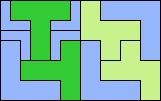
5F+5T+5V 115F+5T+5W 165F+5T+5X ×5F+5T+5Y 55F+5T+5Z ×
5F+5U+5V 65F+5U+5W 65F+5U+5X 95F+5U+5Y 65F+5U+5Z 9
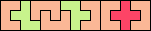
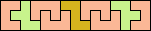
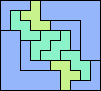
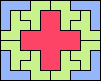
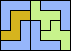
5F+5V+5W 125F+5V+5X 135F+5V+5Y 45F+5V+5Z 75F+5W+5X ×
5F+5W+5Y 85F+5W+5Z ×5F+5X+5Y 65F+5X+5Z ×5F+5Y+5Z 6
5I+5L+5N 55I+5L+5P 45I+5L+5T 55I+5L+5U 55I+5L+5V 4
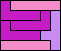
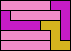
5I+5L+5W 55I+5L+5X 65I+5L+5Y 65I+5L+5Z 75I+5N+5P 5
5I+5N+5T 65I+5N+5U 55I+5N+5V 55I+5N+5W 125I+5N+5X 17
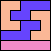
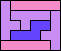
5I+5N+5Y 65I+5N+5Z 115I+5P+5T 45I+5P+5U 55I+5P+5V 4
5I+5P+5W 55I+5P+5X 65I+5P+5Y 45I+5P+5Z 45I+5T+5U 11
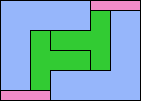
5I+5T+5V 65I+5T+5W 75I+5T+5X 175I+5T+5Y 55I+5T+5Z 12
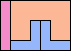
5I+5U+5V 45I+5U+5W 155I+5U+5X 45I+5U+5Y 65I+5U+5Z 7
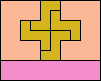
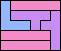
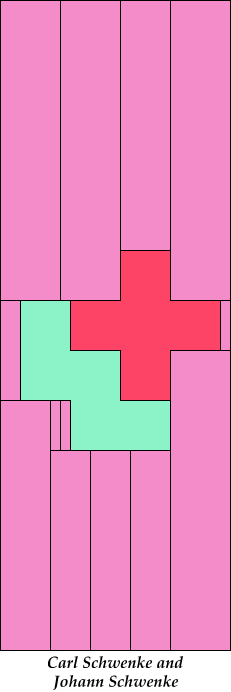
5I+5V+5W 105I+5V+5X 115I+5V+5Y 65I+5V+5Z 45I+5W+5X 21
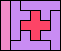
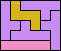
5I+5W+5Y 65I+5W+5Z 115I+5X+5Y 65I+5X+5Z 165I+5Y+5Z 6
5L+5N+5P 45L+5N+5T 65L+5N+5U 55L+5N+5V 35L+5N+5W 6
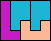
5L+5N+5X 75L+5N+5Y 45L+5N+5Z 55L+5P+5T 45L+5P+5U 4
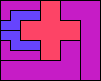
5L+5P+5V 35L+5P+5W 55L+5P+5X 75L+5P+5Y 45L+5P+5Z 4
5L+5T+5U 85L+5T+5V 65L+5T+5W 85L+5T+5X 65L+5T+5Y 3
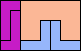
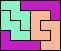
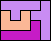
5L+5T+5Z 55L+5U+5V 55L+5U+5W 65L+5U+5X 45L+5U+5Y 4
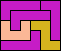
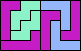
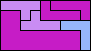
5L+5U+5Z 65L+5V+5W 85L+5V+5X 75L+5V+5Y 65L+5V+5Z 5
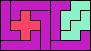
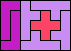
5L+5W+5X 95L+5W+5Y 65L+5W+5Z 95L+5X+5Y 75L+5X+5Z 9
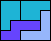
5L+5Y+5Z 55N+5P+5T 65N+5P+5U 35N+5P+5V 45N+5P+5W 6
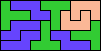
5N+5P+5X 85N+5P+5Y 45N+5P+5Z 65N+5T+5U 105N+5T+5V 7
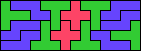
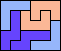
5N+5T+5W 105N+5T+5X 145N+5T+5Y 55N+5T+5Z 135N+5U+5V 6
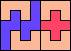
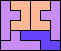
5N+5U+5W 125N+5U+5X 75N+5U+5Y 65N+5U+5Z 65N+5V+5W 6
5N+5V+5X 135N+5V+5Y 55N+5V+5Z 65N+5W+5X ×5N+5W+5Y 8
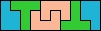
5N+5W+5Z ×5N+5X+5Y 85N+5X+5Z ×5N+5Y+5Z 75P+5T+5U 6
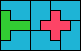
5P+5T+5V 45P+5T+5W 65P+5T+5X 85P+5T+5Y 45P+5T+5Z 6
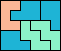
5P+5U+5V 35P+5U+5W 65P+5U+5X 55P+5U+5Y 35P+5U+5Z 5
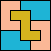
5P+5V+5W 65P+5V+5X 75P+5V+5Y 45P+5V+5Z 45P+5W+5X 7
5P+5W+5Y 55P+5W+5Z 65P+5X+5Y 65P+5X+5Z 85P+5Y+5Z 4
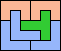
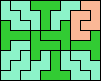
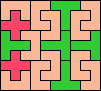
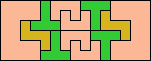
5T+5U+5V 65T+5U+5W 165T+5U+5X 185T+5U+5Y 45T+5U+5Z 12
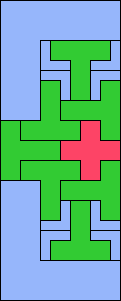
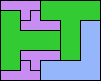
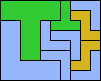
5T+5V+5W 115T+5V+5X 185T+5V+5Y 75T+5V+5Z 105T+5W+5X 20
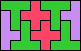
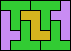
5T+5W+5Y 65T+5W+5Z 165T+5X+5Y 85T+5X+5Z ×5T+5Y+5Z 7
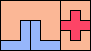
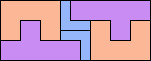
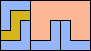
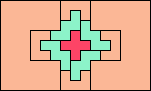
5U+5V+5W 175U+5V+5X 65U+5V+5Y 65U+5V+5Z 65U+5W+5X 11
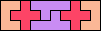
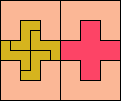
5U+5W+5Y 65U+5W+5Z 125U+5X+5Y 65U+5X+5Z 95U+5Y+5Z 7
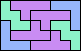
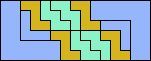
5V+5W+5X 375V+5W+5Y 85V+5W+5Z 125V+5X+5Y 95V+5X+5Z 9
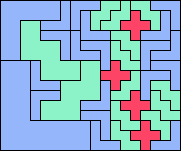
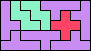
5V+5Y+5Z 45W+5X+5Y 95W+5X+5Z ×5W+5Y+5Z 85X+5Y+5Z 9

Last revised 2022-12-18.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]