Scaled Pentomino Pairs Tiling a Rectangle with the Four Corner Cells
Removed
A pentomino is a figure made of five squares joined
edge to edge.
There are 12 such figures, not distinguishing reflections and rotations.
They were first enumerated and studied by Solomon Golomb.
Here I study the problem of arranging copies of two pentominoes
at various scales
to form a rectangle with the four corner cells removed.
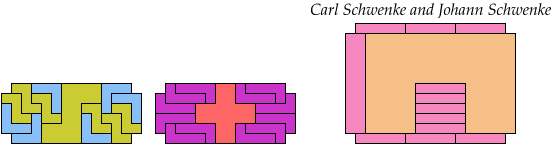
Carl Schwenke and Johann Schwenke improved on two of my solutions.
See also
I use Solomon W. Golomb's original names for the pentominoes:
 This table shows the smallest total number of copies
of two scaled pentominoes known to be
able to tile a rectangle with four of its corner cells removed,
using at least one copy of each pentomino.
This table shows the smallest total number of copies
of two scaled pentominoes known to be
able to tile a rectangle with four of its corner cells removed,
using at least one copy of each pentomino.
| F | I | L | N | P | T | U | V | W | X | Y | Z |
|---|
| F
| *
| 12
| 10
| 4
| 4
| 34
| 4
| 10
| 4
| ×
| 10
| ×
|
|---|
| I
| 12
| *
| 6
| 9
| 5
| 12
| 13
| 9
| 19
| 4
| 4
| 12
|
|---|
| L
| 10
| 6
| *
| 6
| 4
| 10
| 4
| 10
| 8
| 13
| 6
| 10
|
|---|
| N
| 4
| 9
| 6
| *
| 4
| 9
| 10
| 16
| 10
| 9
| 4
| 10
|
|---|
| P
| 4
| 5
| 4
| 4
| *
| 4
| 7
| 4
| 4
| 9
| 4
| 7
|
|---|
| T
| 34
| 12
| 10
| 9
| 4
| *
| 10
| 72
| 10
| ×
| 20
| ×
|
|---|
| U
| 4
| 13
| 4
| 10
| 7
| 10
| *
| 40
| 8
| 4
| 8
| 46
|
|---|
| V
| 10
| 9
| 10
| 16
| 4
| 72
| 40
| *
| 12
| ×
| 10
| 13
|
|---|
| W
| 4
| 19
| 8
| 10
| 4
| 10
| 8
| 12
| *
| 9
| 8
| 52
|
|---|
| X
| ×
| 4
| 13
| 9
| 9
| ×
| 4
| ×
| 9
| *
| 4
| ×
|
|---|
| Y
| 10
| 4
| 6
| 4
| 4
| 20
| 8
| 10
| 8
| 4
| *
| 12
|
|---|
| Z
| ×
| 12
| 10
| 10
| 7
| ×
| 46
| 13
| 52
| ×
| 12
| *
|
|---|
So far as I know, these solutions
use as few tiles as possible. They are not necessarily uniquely minimal.
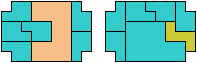
4 Tiles

5 Tiles

6 Tiles

7 Tiles
8 Tiles

9 Tiles

10 Tiles
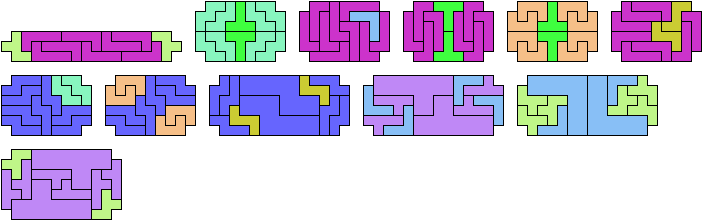
12 Tiles

13 Tiles
16 Tiles

19 Tiles
20 Tiles
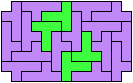
34 Tiles
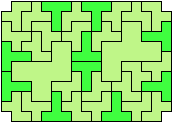
40 Tiles
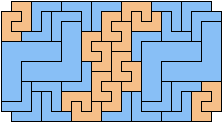
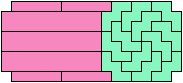
46 Tiles

52 Tiles
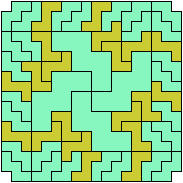
72 Tiles

Last revised 2024-02-27.
Back to Polyomino and Polyking Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]


















