




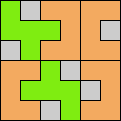


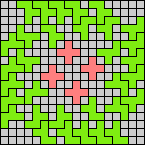

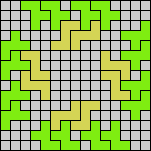

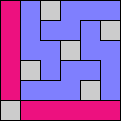
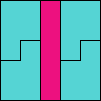
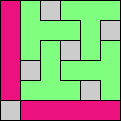
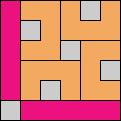
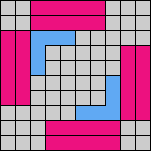
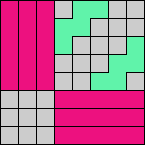

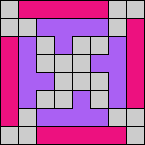



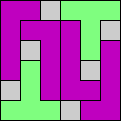
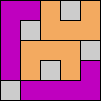
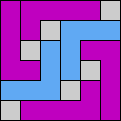


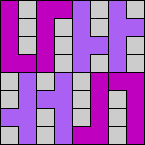






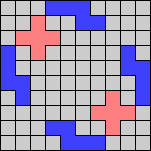

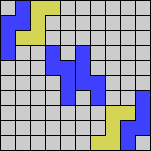

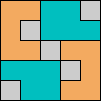





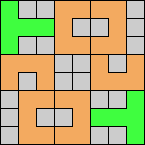
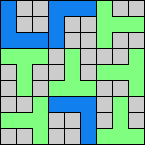

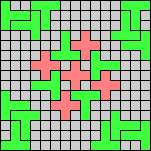
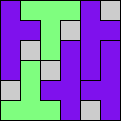
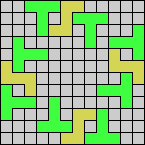
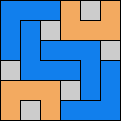
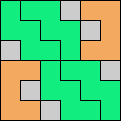

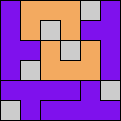

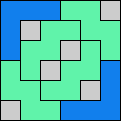

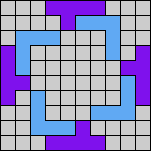

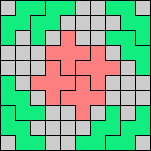



Issue 34 of Rodolfo Marcelo Kurchan's Puzzle Fun extended this work, showing minimal solutions for various numbers of cells and for single sets of the polyominoes of a given size.
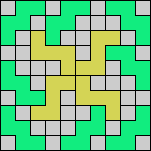
Here I show magic squares for pairs of pentominoes, using at least one copy of each. As in Math Magic, solutions have as few tiles as are known to be possible.
| 5F + 5I | 5F + 5L | 5F + 5N | 5F + 5P | 5F + 5T | 5F + 5U |
|---|---|---|---|---|---|
 |  |  |  |  |  |
| 5F + 5V | 5F + 5W | 5F + 5X | 5F + 5Y | 5F + 5Z | 5I + 5L |
 |  |  |  |  |  |
| 5I + 5N | 5I + 5P | 5I + 5T | 5I + 5U | 5I + 5V | 5I + 5W |
 | 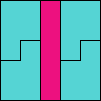 |  |  |  |  |
| 5I + 5X | 5I + 5Y | 5I + 5Z | 5L + 5N | 5L + 5P | 5L + 5T |
 |  |  |  |  |  |
| 5L + 5U | 5L + 5V | 5L + 5W | 5L + 5X | 5L + 5Y | 5L + 5Z |
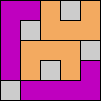 |  |  |  |  |  |
| 5N + 5P | 5N + 5T | 5N + 5U | 5N + 5V | 5N + 5W | 5N + 5X |
 |  |  |  |  |  |
| 5N + 5Y | 5N + 5Z | 5P + 5T | 5P + 5U | 5P + 5V | 5P + 5W |
 |  |  | 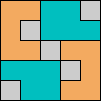 |  |  |
| 5P + 5X | 5P + 5Y | 5P + 5Z | 5T + 5U | 5T + 5V | 5T + 5W |
 |  |  |  |  |  |
| 5T + 5X | 5T + 5Y | 5T + 5Z | 5U + 5V | 5U + 5W | 5U + 5X |
 |  |  |  |  |  |
| 5U + 5Y | 5U + 5Z | 5V + 5W | 5V + 5X | 5V + 5Y | 5V + 5Z |
 |  |  |  |  |  |
| 5W + 5X | 5W + 5Y | 5W + 5Z | 5X + 5Y | 5X + 5Z | 5Y + 5Z |
 |  |  |  |  |
Last revised 2021-09-09.