Baiocchi Figures for Tetromino-Pentomino Pairs
A Baiocchi figure is a figure
formed by joining copies of a polyform and having the maximal
symmetry for the polyform's class.
For polyominoes, that means square symmetry, or 4-way rotary with reflection.
If a polyomino lacks diagonal symmetry, its Baiocchi figures
must be Galvagni figures or contain Galvagni figures.
Claudio
Baiocchi proposed the idea in January 2008.
Baiocchi figures first appeared in Erich Friedman's
Math Magic for that month.
We can also define Baiocchi Figures for sets of polyominoes.
Here I show minimal known Baiocchi Figures for pairs consisting of
a tetromino and a pentomino.
The figures must use at least one copy of each polyomino.
See also
Baiocchi Figures
for Pentomino Pairs
and
Baiocchi Figures
for Hexomino Pairs.
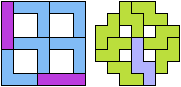
9 Cells

13 Cells
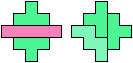
17 Cells
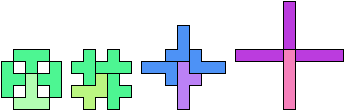
21 Cells
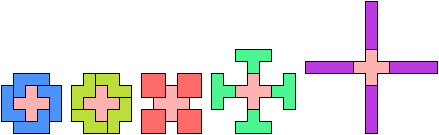
24 Cells

25 Cells

28 Cells
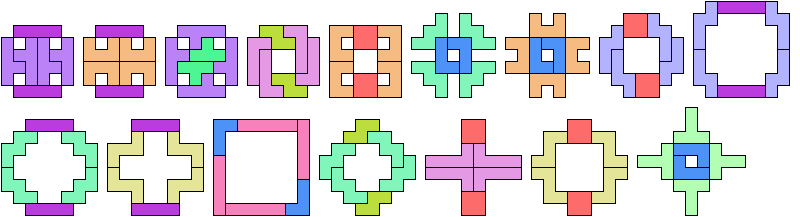
33 Cells
36 Cells
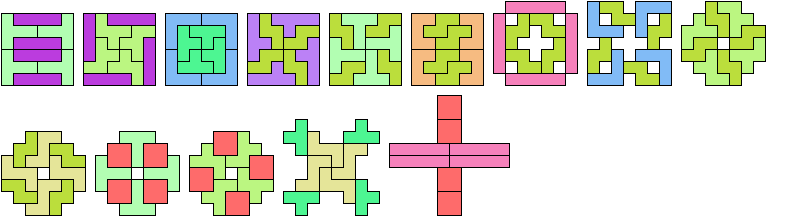 Holeless solutions shown above are not reproduced here.
Holeless solutions shown above are not reproduced here.
21 Cells
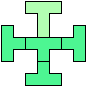
28 Cells
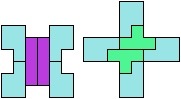
32 Cells
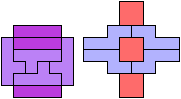
33 Cells
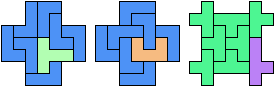
36 Cells

37 Cells
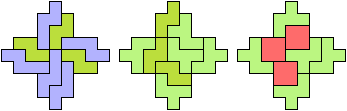
44 Cells
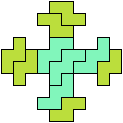
52 Cells
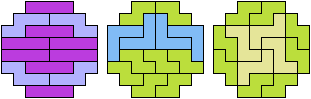
56 Cells
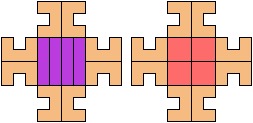
57 Cells
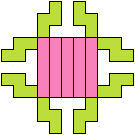
60 Cells
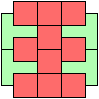
Last revised 2023-10-09.
Back to Baiocchi Figures
<
Polyform Compatibility
<
Polyform Curiosities
George Sicherman
[ HOME
| MAIL
]



















