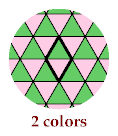
Polyominoes on a Multicolored Infinite Grid(in Thane Plambeck and Tomas Rokicki, eds., Barrycades and Septoku: Papers in Honor of Martin Gardner and Tom Rogers, Providence, 2020, MAA Press, Spectrum Series, v. 100, pp. 29–36), Hans Hung-Hsun Yu investigates how many colors are needed for the cells of the plane to ensure that a given polyomino has no two cells of the same color. Here I consider the corresponding problem for polyiamonds.
A polyiamond with k cells requires at least k colors. In the diagrams below, color counts that exactly meet this requirement appear in red.
For polyhexes, see Polyhex Variegation.
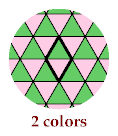
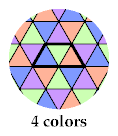
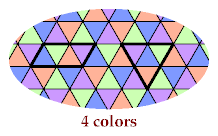
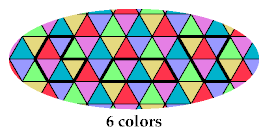
The third tetriamond requires 6 colors, to distinguish the cells of a hexagon with side 1:
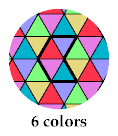
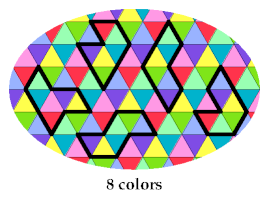
The fourth pentiamond requires 8 colors:

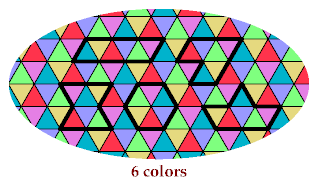
The pattern for the J pentiamond admits five other hexiamonds:
Here is the best pattern I have found for the remaining two hexiamonds.
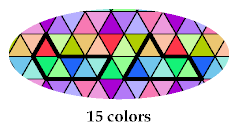
Last revised 2018-07-19.