
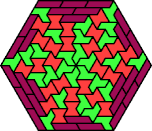
It has long been known that eight hexiamonds can tile regular hexagons:

Here I study the related problem of tiling some regular hexagon with three hexiamonds, using the same number of copies of each.
For two hexiamonds, see Two-Hexiamond Balanced Hexagons.
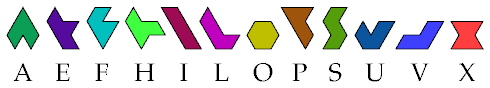
| A E F | 36 | A E H | 81 | A E I | ? | A E L | 9 | A E O | ? | A E P | 36 | A E S | 36 | A E U | 9 | A E V | 36 | A E X | ? |
| A F H | 36 | A F I | 36 | A F L | 36 | A F O | ? | A F P | 36 | A F S | 36 | A F U | 36 | A F V | 36 | A F X | 144 | A H I | 9 |
| A H L | 9 | A H O | 36 | A H P | 36 | A H S | 81 | A H U | 36 | A H V | 36 | A H X | 324 | A I L | 36 | A I O | ? | A I P | 36 |
| A I S | 36 | A I U | 9 | A I V | 36 | A I X | ? | A L O | 9 | A L P | 36 | A L S | 9 | A L U | 9 | A L V | 9 | A L X | 36 |
| A O P | 36 | A O S | 324 | A O U | 144 | A O V | 36 | A O X | 144 | A P S | 36 | A P U | 36 | A P V | 36 | A P X | 36 | A S U | 36 |
| A S V | 36 | A S X | ? | A U V | 9 | A U X | 36 | A V X | 81 | E F H | 36 | E F I | 36 | E F L | 36 | E F O | 144 | E F P | 9 |
| E F S | 36 | E F U | 36 | E F V | 36 | E F X | ? | E H I | 36 | E H L | 36 | E H O | ? | E H P | 36 | E H S | 36 | E H U | 9 |
| E H V | 36 | E H X | ? | E I L | 9 | E I O | ? | E I P | 36 | E I S | 36 | E I U | 36 | E I V | 36 | E I X | ? | E L O | 9 |
| E L P | 36 | E L S | 9 | E L U | 9 | E L V | 9 | E L X | ? | E O P | 36 | E O S | ? | E O U | ? | E O V | 36 | E O X | ? |
| E P S | 36 | E P U | 36 | E P V | 36 | E P X | ? | E S U | 9 | E S V | 9 | E S X | ? | E U V | 36 | E U X | 81 | E V X | ? |
| F H I | 36 | F H L | 36 | F H O | 36 | F H P | 36 | F H S | 36 | F H U | 36 | F H V | 36 | F H X | 36 | F I L | 36 | F I O | ? |
| F I P | 9 | F I S | 36 | F I U | 36 | F I V | 36 | F I X | 36 | F L O | 36 | F L P | 9 | F L S | 36 | F L U | 36 | F L V | 36 |
| F L X | 36 | F O P | 36 | F O S | 144 | F O U | 144 | F O V | 36 | F O X | 144 | F P S | 36 | F P U | 9 | F P V | 36 | F P X | 36 |
| F S U | 36 | F S V | 36 | F S X | 144 | F U V | 36 | F U X | 36 | F V X | 36 | H I L | 36 | H I O | 9 | H I P | 36 | H I S | 9 |
| H I U | 9 | H I V | 9 | H I X | 81 | H L O | 9 | H L P | 36 | H L S | 36 | H L U | 9 | H L V | 9 | H L X | 36 | H O P | 36 |
| H O S | 9 | H O U | 36 | H O V | 36 | H O X | 144 | H P S | 36 | H P U | 36 | H P V | 36 | H P X | 36 | H S U | 36 | H S V | 9 |
| H S X | ? | H U V | 9 | H U X | 36 | H V X | 81 | I L O | 36 | I L P | 36 | I L S | 9 | I L U | 36 | I L V | 36 | I L X | 81 |
| I O P | 36 | I O S | ? | I O U | 81 | I O V | 9 | I O X | 144 | I P S | 36 | I P U | 36 | I P V | 36 | I P X | 36 | I S U | 36 |
| I S V | 9 | I S X | 144 | I U V | 9 | I U X | 9 | I V X | 9 | L O P | 36 | L O S | ? | L O U | ? | L O V | 36 | L O X | 81 |
| L P S | 36 | L P U | 36 | L P V | 36 | L P X | 36 | L S U | 9 | L S V | 36 | L S X | 144 | L U V | 36 | L U X | 36 | L V X | 36 |
| O P S | 36 | O P U | 36 | O P V | 36 | O P X | 36 | O S U | ? | O S V | 9 | O S X | ? | O U V | 9 | O U X | 81 | O V X | 36 |
| P S U | 36 | P S V | 36 | P S X | 36 | P U V | 36 | P U X | 36 | P V X | 36 | S U V | 36 | S U X | 36 | S V X | 324 | U V X | 36 |
| 6A+6E+6F | 6A+6E+6H | 6A+6E+6I | 6A+6E+6L | 6A+6E+6O |
|---|---|---|---|---|

| 
| 
| 
| 
|
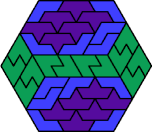
| 6A+6E+6P | 6A+6E+6S | 6A+6E+6U | 6A+6E+6V | 6A+6E+6X |

| 
| 
| 
| 
|
| 6A+6F+6H | 6A+6F+6I | 6A+6F+6L | 6A+6F+6O | 6A+6F+6P |

| 
| 
| 
| 
|
| 6A+6F+6S | 6A+6F+6U | 6A+6F+6V | 6A+6F+6X | 6A+6H+6I |

| 
| 
| 
| 
|
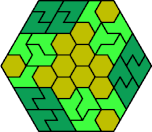
| 6A+6H+6L | 6A+6H+6O | 6A+6H+6P | 6A+6H+6S | 6A+6H+6U |

| 
| 
| 
| 
|
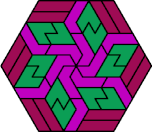
| 6A+6H+6V | 6A+6H+6X | 6A+6I+6L | 6A+6I+6O | 6A+6I+6P |

| 
| 
| 
| 
|
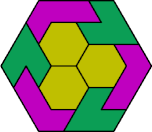
| 6A+6I+6S | 6A+6I+6U | 6A+6I+6V | 6A+6I+6X | 6A+6L+6O |

| 
| 
| 
| 
|
| 6A+6L+6P | 6A+6L+6S | 6A+6L+6U | 6A+6L+6V | 6A+6L+6X |

| 
| 
| 
| 
|
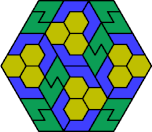
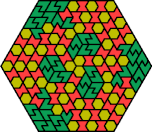
| 6A+6O+6P | 6A+6O+6S | 6A+6O+6U | 6A+6O+6V | 6A+6O+6X |

| 
| 
| 
| 
|
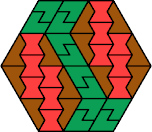
| 6A+6P+6S | 6A+6P+6U | 6A+6P+6V | 6A+6P+6X | 6A+6S+6U |

| 
| 
| 
| 
|
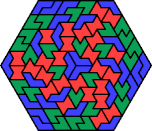
| 6A+6S+6V | 6A+6S+6X | 6A+6U+6V | 6A+6U+6X | 6A+6V+6X |

| 
| 
| 
| 
|
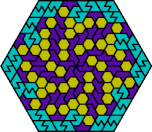
| 6E+6F+6H | 6E+6F+6I | 6E+6F+6L | 6E+6F+6O | 6E+6F+6P |

| 
| 
| 
| 
|
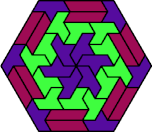
| 6E+6F+6S | 6E+6F+6U | 6E+6F+6V | 6E+6F+6X | 6E+6H+6I |

| 
| 
| 
| 
|
| 6E+6H+6L | 6E+6H+6O | 6E+6H+6P | 6E+6H+6S | 6E+6H+6U |

| 
| 
| 
| 
|
| 6E+6H+6V | 6E+6H+6X | 6E+6I+6L | 6E+6I+6O | 6E+6I+6P |

| 
| 
| 
| 
|
| 6E+6I+6S | 6E+6I+6U | 6E+6I+6V | 6E+6I+6X | 6E+6L+6O |

| 
| 
| 
| 
|
| 6E+6L+6P | 6E+6L+6S | 6E+6L+6U | 6E+6L+6V | 6E+6L+6X |

| 
| 
| 
| 
|
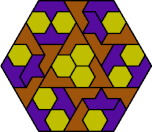
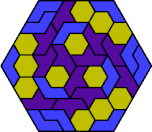
| 6E+6O+6P | 6E+6O+6S | 6E+6O+6U | 6E+6O+6V | 6E+6O+6X |
| 
| 
| 
| 
|
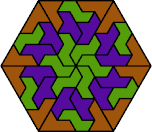
| 6E+6P+6S | 6E+6P+6U | 6E+6P+6V | 6E+6P+6X | 6E+6S+6U |
| 
| 
| 
| 
|
| 6E+6S+6V | 6E+6S+6X | 6E+6U+6V | 6E+6U+6X | 6E+6V+6X |

| 
| 
| 
| 
|
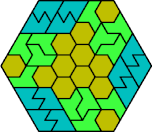
| 6F+6H+6I | 6F+6H+6L | 6F+6H+6O | 6F+6H+6P | 6F+6H+6S |

| 
| 
| 
| 
|
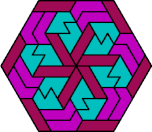
| 6F+6H+6U | 6F+6H+6V | 6F+6H+6X | 6F+6I+6L | 6F+6I+6O |

| 
| 
| 
| 
|
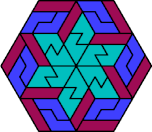
| 6F+6I+6P | 6F+6I+6S | 6F+6I+6U | 6F+6I+6V | 6F+6I+6X |

| 
| 
| 
| 
|
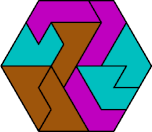
| 6F+6L+6O | 6F+6L+6P | 6F+6L+6S | 6F+6L+6U | 6F+6L+6V |

| 
| 
| 
| 
|
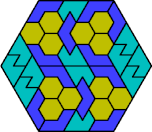
| 6F+6L+6X | 6F+6O+6P | 6F+6O+6S | 6F+6O+6U | 6F+6O+6V |

| 
| 
| 
| 
|
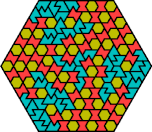
| 6F+6O+6X | 6F+6P+6S | 6F+6P+6U | 6F+6P+6V | 6F+6P+6X |
| 
| 
| 
| 
|
| 6F+6S+6U | 6F+6S+6V | 6F+6S+6X | 6F+6U+6V | 6F+6U+6X |

| 
| 
| 
| 
|
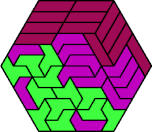
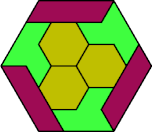
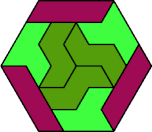
| 6F+6V+6X | 6H+6I+6L | 6H+6I+6O | 6H+6I+6P | 6H+6I+6S |

| 
| 
| 
| 
|
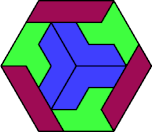
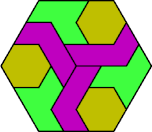
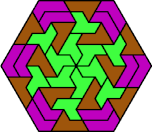
| 6H+6I+6U | 6H+6I+6V | 6H+6I+6X | 6H+6L+6O | 6H+6L+6P |

| 
| 
| 
| 
|
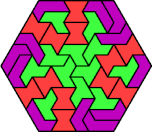
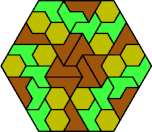
| 6H+6L+6S | 6H+6L+6U | 6H+6L+6V | 6H+6L+6X | 6H+6O+6P |

| 
| 
| 
| 
|
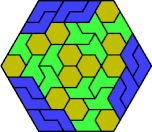
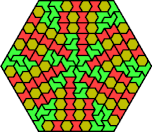
| 6H+6O+6S | 6H+6O+6U | 6H+6O+6V | 6H+6O+6X | 6H+6P+6S |

| 
| 
| 
| 
|
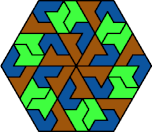
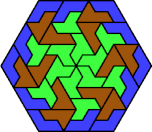
| 6H+6P+6U | 6H+6P+6V | 6H+6P+6X | 6H+6S+6U | 6H+6S+6V |
| 
| 
| 
| 
|
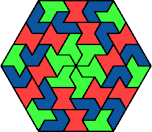
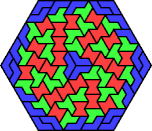
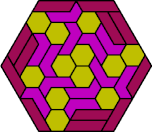
| 6H+6S+6X | 6H+6U+6V | 6H+6U+6X | 6H+6V+6X | 6I+6L+6O |

| 
| 
| 
| 
|
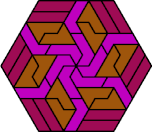
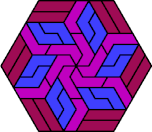
| 6I+6L+6P | 6I+6L+6S | 6I+6L+6U | 6I+6L+6V | 6I+6L+6X |
| 
| 
| 
| 
|
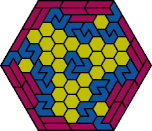
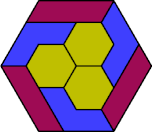
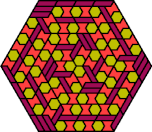
| 6I+6O+6P | 6I+6O+6S | 6I+6O+6U | 6I+6O+6V | 6I+6O+6X |

| 
| 
| 
| 
|
| 6I+6P+6S | 6I+6P+6U | 6I+6P+6V | 6I+6P+6X | 6I+6S+6U |

| 
| 
| 
| 
|
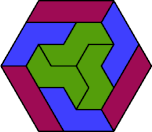
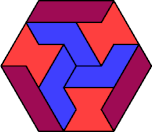
| 6I+6S+6V | 6I+6S+6X | 6I+6U+6V | 6I+6U+6X | 6I+6V+6X |
| 
| 
| 
| 
|
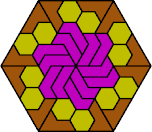
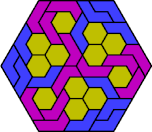
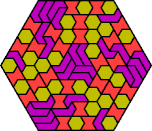
| 6L+6O+6P | 6L+6O+6S | 6L+6O+6U | 6L+6O+6V | 6L+6O+6X |
| 
| 
| 
| 
|
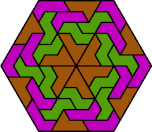
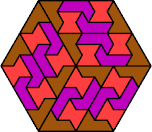
| 6L+6P+6S | 6L+6P+6U | 6L+6P+6V | 6L+6P+6X | 6L+6S+6U |
| 
| 
| 
| 
|
| 6L+6S+6V | 6L+6S+6X | 6L+6U+6V | 6L+6U+6X | 6L+6V+6X |

| 
| 
| 
| 
|
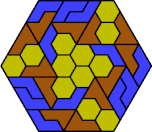
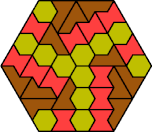
| 6O+6P+6S | 6O+6P+6U | 6O+6P+6V | 6O+6P+6X | 6O+6S+6U |

| 
| 
| 
| 
|
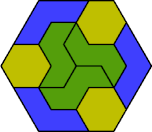
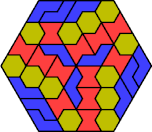
| 6O+6S+6V | 6O+6S+6X | 6O+6U+6V | 6O+6U+6X | 6O+6V+6X |
| 
| 
| 
| 
|
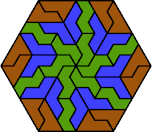
| 6P+6S+6U | 6P+6S+6V | 6P+6S+6X | 6P+6U+6V | 6P+6U+6X |

| 
| 
| 
| 
|
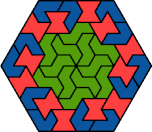
| 6P+6V+6X | 6S+6U+6V | 6S+6U+6X | 6S+6V+6X | 6U+6V+6X |

| 
| 
| 
| 
|
Last revised 2012-07-04.