Pentiamond Compatibility
Introduction
A pentiamond is a plane figure made of five
equilateral triangles joined edge to edge.
There are 4 such figures, not distinguishing reflections and rotations.
The compatibility problem
is to find a figure that can be tiled with each of a set of polyforms.
Polyomino compatibility has been widely studied since the early 1990s.
Polyiamond compatibility was first studied systematically
by Margarita Lukjanska and Andris Cibulis,
who published a paper about it with Andy Liu in 2005 in the Journal
of Recreational Mathematics.
This web page and my other page, Mixed
Polyiamond Compatibility, extend and correct the solutions in
the JRM article.
See also Zucca's Challenge
Problem for Polyiamonds.
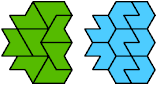
Solutions
Here are minimal compatibility figures for pairs
of pentiamonds.
These solutions are not necessarily unique.

Horizontally Symmetric Variant
This variant solution has horizontal mirror symmetry:

Holeless Variant
The minimal solution for the Q and U pentiamonds has a hole.
Here is the minimal holeless solution:
Last revised 2022-12-31.
Back to Pairwise Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]



