where T(k) is the kth triangular number.
This formula implies that a square with side T(k)
might be dissected into 1 square of side 1, 2 squares of side 2,
and so on up to k squares of side k.
Such a tiling is a partridge tiling,
named after the partridge in the song The Twelve Days of Christmas.
It was first proposed and discovered by Robert Wainwright.
See the August 2002
issue
of Erich Friedman's Math Magic
for a survey of known partridge tilings.
In 2021 I introduced lovebirds tilings. These use a double set of copies of a shape, with scale factors 1…k, to construct two copies of the shape at scale T(k).
Any plane shape with a partridge tiling can use two copies of the tiling to form a lovebirds tiling. Here I show polyforms that can form lovebirds tilings but not partridge tilings, or can form lovebirds tilings with fewer sizes of tiles than their smallest known partridge tilings. If you find a new lovebirds tiling with this property, please write.
The domino has partridge number 7. It has lovebirds number 3:
It follows that any parallelogram with sides in the ratio 1:2 has a lovebirds number of 3 or less. This includes the straight tetriamond.
The I tetromino has partridge number 7. Its lovebirds number is 6:
The L tetromino has no known partridge tiling. Its lovebirds number is 3:
The P hexomino has no known partridge tiling. Its lovebirds number is 3:
The 2×3 rectangle has partridge number 7. It has lovebirds number 3:
The 3×4 rectangle has partridge number 7. It has lovebirds number 3:
The 3×8 rectangle has partridge number 7. It has lovebirds number 6:

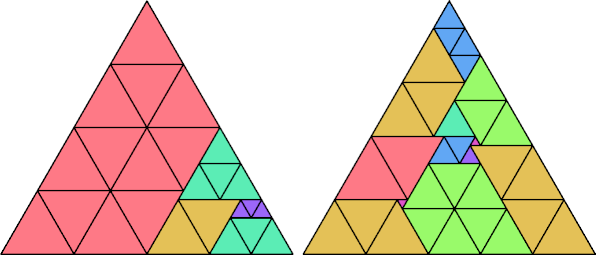
It follows that any triangle has lovebirds number 7 or less.
Bryce Herdt points out that the triamond has lovebirds number 3:
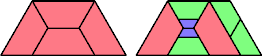
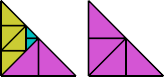
From this Erich deduced that the lovebirds number of any right triangle is at most 3.
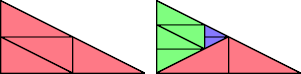
This tridom has partridge number 6. Its lovebirds number is 4:
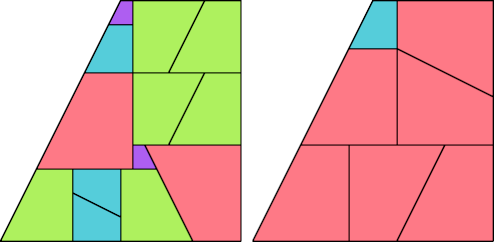
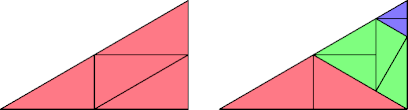
This tridrafter has partridge number 6 and lovebirds number 3:
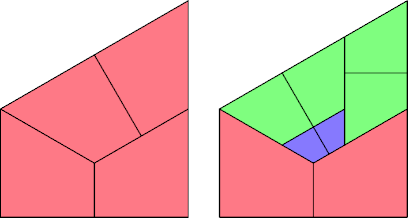
Last revised 2025-10-04.