In 2000 Livio Zucca published a web page with this conjecture (paraphrased):
Define an island in a polydom tiling as a connected subtiling in the shape of an oblique polyomino, such that the tiles outside the island lie on the polyomino grid and the tiles inside the island lie on the oblique reflected grid. Then the polyomino shape of the island must be a polydomino; that is, a polyomino that can be tiled by dominoes.
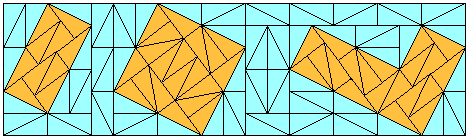
Zucca gives three examples, shown below:

It is not hard to show that the oblique T tetromino, the only tetromino that cannot be tiled with dominoes, cannot be tiled with monodoms on the reflected grid.
But there is a counterexample to Zucca's conjecture! The smallest is the twist hexomino. It cannot be tiled with dominoes, and it can form an island:
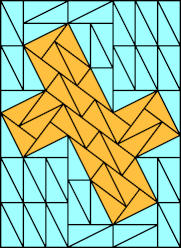
We may define an island prime as a one-sided (non-reflecting) polyomino that when scaled up by a factor of √5 can be tiled with monodoms in the orientations shown, and at its original scale cannot be tiled by any combination of smaller island primes. These polyominoes are the smallest island primes:
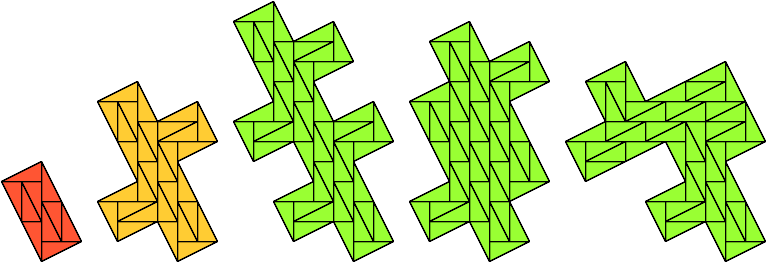
Are there infinitely many island primes?
Last revised 2020-07-02.