Catalogue of Convex Polydrafters

Introduction

A polydrafter is a polyform made by joining equal drafters, 30°-60°-90° right triangles, at their short legs, long legs, hypotenuses, or half hypotenuses. Polydrafters whose cells belong to a common polyiamond (triangle) grid are sometimes called proper polydrafters. Polydrafters whose cells depart from the grid are called extended polydrafters. For more information see Wikipedia.

Below I show all convex proper polydrafters with from 1 to 7 cells. The decompositions of the polydrafters into drafter cells are not necessarily unique. The counts and drawings do not include extended polydrafters. If you find an error or omission, please write.

Enumeration

In this enumeration, mirror images are treated as the same polydrafter.

Cells Number

1 1

2 4

3 3

4 7

5 7

6 13

7 9

8 15

9 9

10 14

11 12

12 27

13 19

14 29

15 26

16 29

17 20

18 36

19 26

20 48

Cells	Number
1	1
2	4
3	3
4	7
5	7
6	13
7	9
8	15
9	9
10	14
11	12
12	27
13	19
14	29
15	26
16	29
17	20
18	36
19	26
20	48

Monodrafter

Didrafters

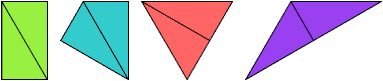
Puzzle: arrange the four convex proper didrafters to make a convex shape. [Solution]

Tridrafters

Tetradrafters

Puzzle: arrange the seven convex proper tetradrafters to make a convex shape. [Solution]

Pentadrafters

Hexadrafters

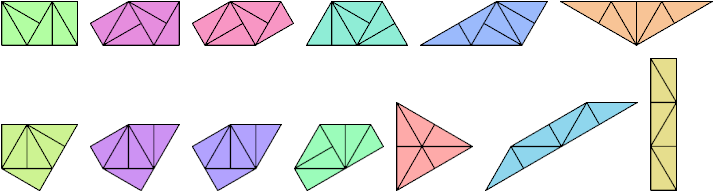
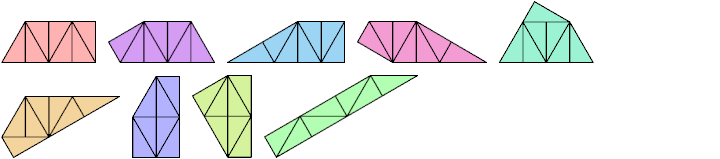
Heptadrafters

Last revised 2024-11-02.

Back to Polyform Catalogues < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]

Cells	Number
1	1
2	4
3	3
4	7
5	7
6	13
7	9
8	15
9	9
10	14
11	12
12	27
13	19
14	29
15	26
16	29
17	20
18	36
19	26
20	48

Cells	Number
1	1
2	4
3	3
4	7
5	7
6	13
7	9
8	15
9	9
10	14
11	12
12	27
13	19
14	29
15	26
16	29
17	20
18	36
19	26
20	48

Cells	Number
1	1
2	4
3	3
4	7
5	7
6	13
7	9
8	15
9	9
10	14
11	12
12	27
13	19
14	29
15	26
16	29
17	20
18	36
19	26
20	48