
The term is due to Andrew Clarke.
The suffix -dom
is half the word domino
,
making it appropriate for a half-domino.
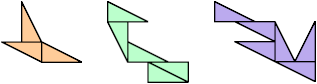
A didom is a polydom with two cells. A short leg of one cell may be adjacent to a long leg of another, and the long legs of two adjacent cells are allowed to overlap halfway. Thus there are 13 different didoms:

The last didom is known as the kite. It is the only didom whose vertices do not all lie on a common square grid. This makes it awkward to use in didom tilings. It must be used in pairs, as seen in Brendan Owen's tiling of a near-regular dodecagon with two sets of 13 didoms. See Bernd Karl Rennhak's Logelium for more constructions using the kite didom.
Polydoms that do not contain kite didoms are called kiteless. Below are various tilings with the kiteless didoms.
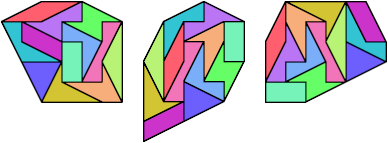
All these shapes have multiple solutions—but none more than five.
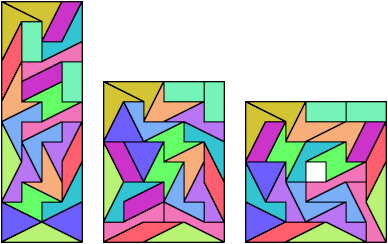
It can also form a hexagon, a rotary octagon, and a decagon:
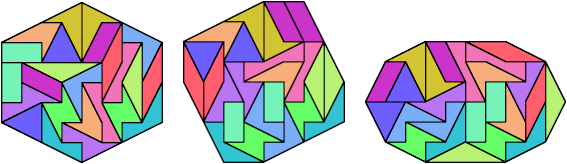
Besides these symmetric shapes, it can form these tridoms scaled up by a factor of four. Most of these tilings were found by Abaroth:

Abaroth also found this triangle with a hole …
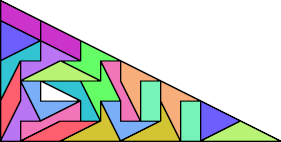
… and many symmetric arrangements of the double set of kiteless didoms. You can download them in PDF format [here] and [here].
Last revised 2018-10-22.