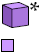
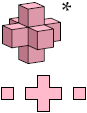
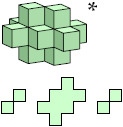
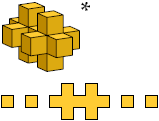
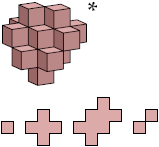
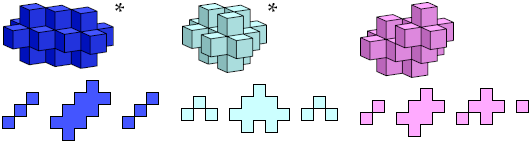
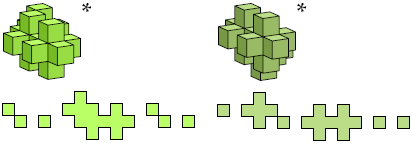
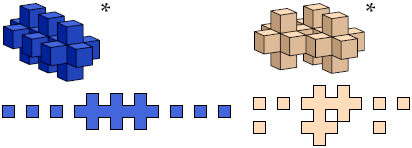
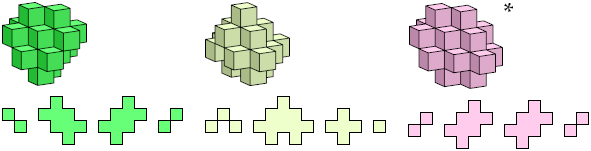
Here I show all unitary polycubes with at most 25 cells. I do not distinguish mirror images. Cross-sections are shown from the bottom up. Unitary polycubes that are known to be able to fill space are marked with an asterisk (*). That which is known to fill space only if it may be reflected is marked with a double dagger (‡).
If you find an omission, please write.
Bryce Herdt identified many space-filling unitary polycubes, and supplied a simple method of proving that a polycube fills space by translation.
| Cells | 1 | 7 | 12 | 13 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polycubes | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 2 | 3 | 4 | 16 | 21 | 19 | 24 |





Last revised 2023-03-19.