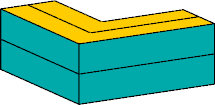
surfaces.Where the ring bends, the surfaces perpendicular to the axis of the bend simply continue around the corresponding corner of the polyomino face. The surfaces parallel to the axis
climbover the inner or outer axis of the bend.

Vélez's best known polycube ring has 22 cells.
It turns so that its cross-section
makes a 90° twist, or quarter turn,
along its full length.
This means that its four surfaces
form one continuous surface.
Vélez's 22-cell
polycube appeared in Martin Gardner's Mathematical Games
column in the August 1978 issue of Scientific American,
and later in Gardner's book
Fractal Music, Hypercards
and More ….
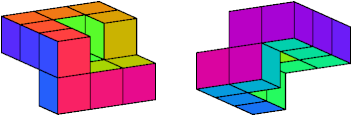
Gardner asked for the smallest such polycube ring
whose surfaces have a quarter turn.
His answer was this ring with just 10 cells:
Vélez and others later made a Wolfram Demonstration
showing both polycubes and their surfaces,
Vélez-Jahn's Möbius Toroidal Polyhedron
.
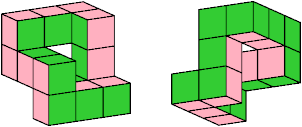
Here is a wooden model of it:

By stretching this half-twist ring, breaching one of the stretched lengths, and joining the ring to a copy of itself, we can get a polycube ring with a full twist:
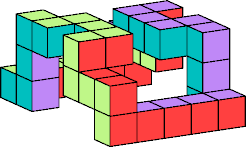
It is likely that a twist of three-quarters can be obtained in a similar way. I do not know the minimal polycube rings for these or other degrees of twisting. So far as I know, this problem is open.
See also Robert Dickau's One-Sided Toroidal Polyhedra.
Last revised 2025-04-07.