Strong Surround Numbers for Polycairos
A polycairo is a plane figure formed by
joining isosceles pentagons in the Cairo
Grid.
The strong surround number of a polycairo
is the lowest number of copies of the polycairo that can surround
it strongly; that is, including its corners.
The polycairos must conform to the Cairo grid.
Strong surround numbers for polyominoes were proposed
by Jaime Poniachik in Issue 8
of Puzzle Fun.
He asked for the smallest polyominoes with a given strong surround number.
In Issue 10,
Rodolfo Kurchan extended the problem
to polyiamonds, polyhexes, and polyaboloes.
He also investigated the smallest polyforms that cannot surround themselves,
and the smallest holeless such polyforms.
However, his results were not complete.
Here I show minimal strong surrounds for small polycairos,
the smallest polycairos with given surround numbers,
and the smallest polycairos with no strong surrounds.
See also
Minimal Strong Surrounds
An exclamation point (!) indicates that the solution is unique for
the minimum number of tiles.
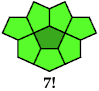
Monocairo
Dicairos
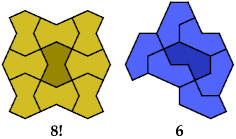
Tricairos
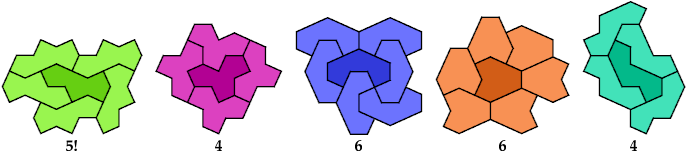
Tetracairos
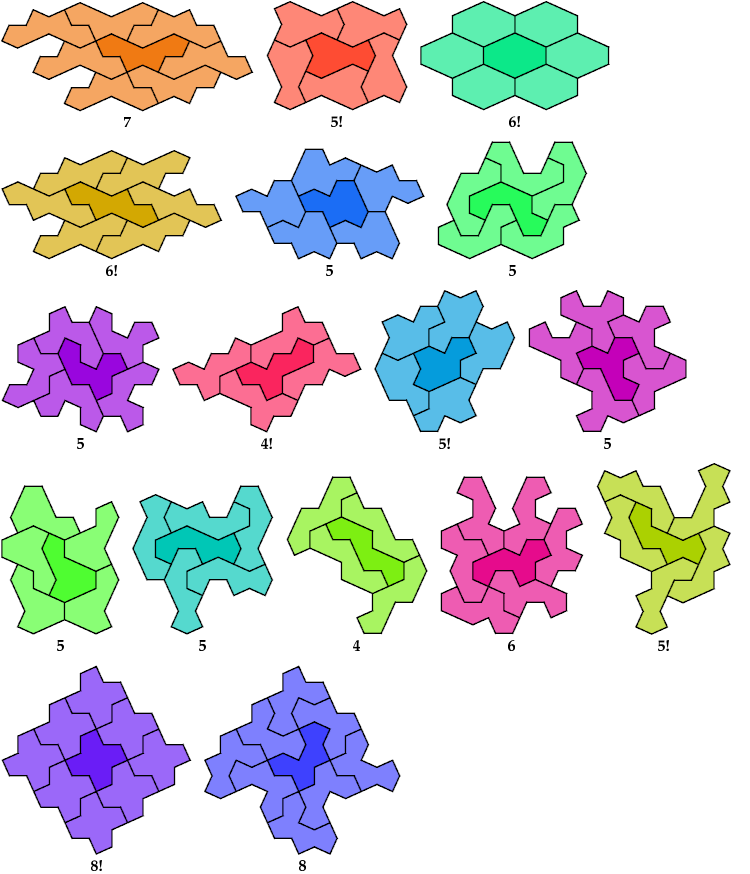
Minimal Polycairos with Given Strong Surround Numbers
3 Copies, 9 Cells
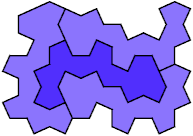
4 Copies, 3 Cells
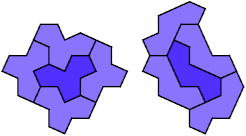
5 Copies, 3 Cells
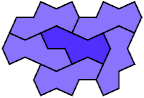
6 Copies, 2 Cells
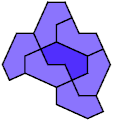
7 Copies, 1 Cell
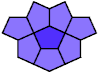
8 Copies, 2 Cells
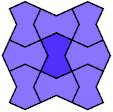
9 Copies, 6 Cells
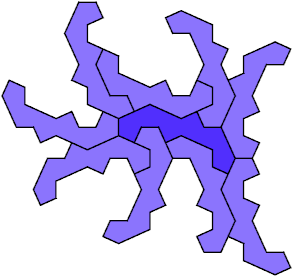
10 Copies, 8 Cells
11 Copies, 8 Cells
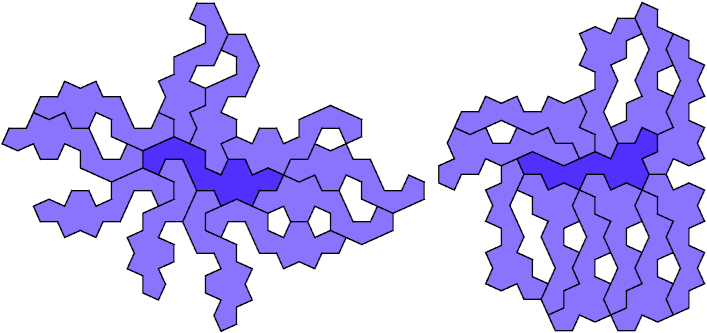
12 Copies, 7 Cells
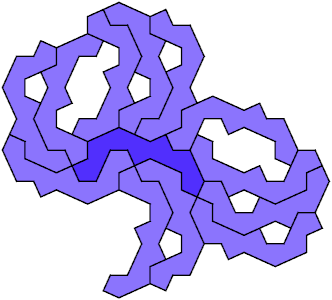
Minimal Polycairos that Cannot Surround Themselves Strongly
Last revised 2023-06-30.
Back to Polyform Surrounding
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]