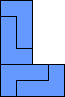

This tiling is said to be rep-4 (or rep-22), because it uses four tiles.
An irreptile is a polyform that can be tiled by smaller copies of itself, not necessarily the same size. This is an irreptiling of the L pentomino by Karl Scherer, who coined the term irreptile and first systematically studied irreptilings:
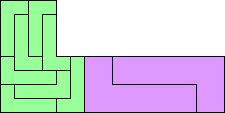
An irreptiling with different-sized tiles is a proper irreptiling. Some polyforms have irreptilings but not reptilings. Others can be irreptiled with fewer tiles than are needed for their smallest reptilings.
Polycubes are polyforms made by joining equal cubes face to face.
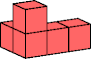
Little is known about polycube reptilings and irreptilings, because computing polycube tilings is lengthy and complex.
Karl Scherer, in his Wolfram Demonstration of polycube reptilings and irreptilings, asks which polycubes can be irreptiled using fewer tiles than their smallest reptilings. Here I show some polycubes with this property. If you find a solution with fewer tiles, or a solution for a polycube not shown here, please write!
See also Polycube Reptiles.
In the results below, polycubes may not be reflected.
Click on a polycube to see its smallest known irreptiling.
Bryce Herdt improved on one of my tilings. (I later improved on his.)
No proper minimal irreptiling of a polycube with fewer than 20 tiles is known.
Last revised 2021-03-22.