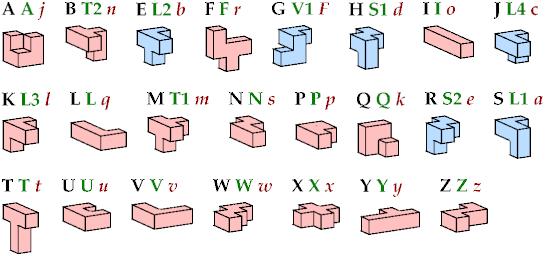

The letters shown in black are my names. Mirror images of chiral pentacubes are indicated with ′; e.g., G′ is the mirror image of G. The green symbols are Kate Jones's names. The red symbols are Donald Knuth's names.
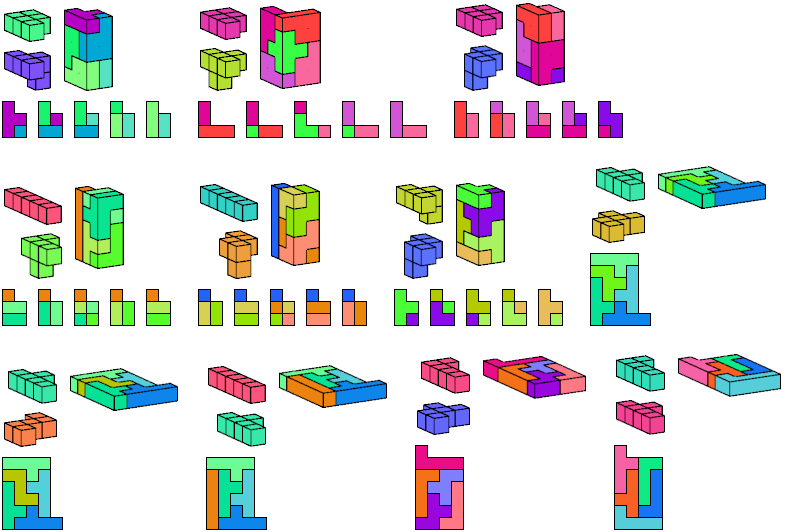
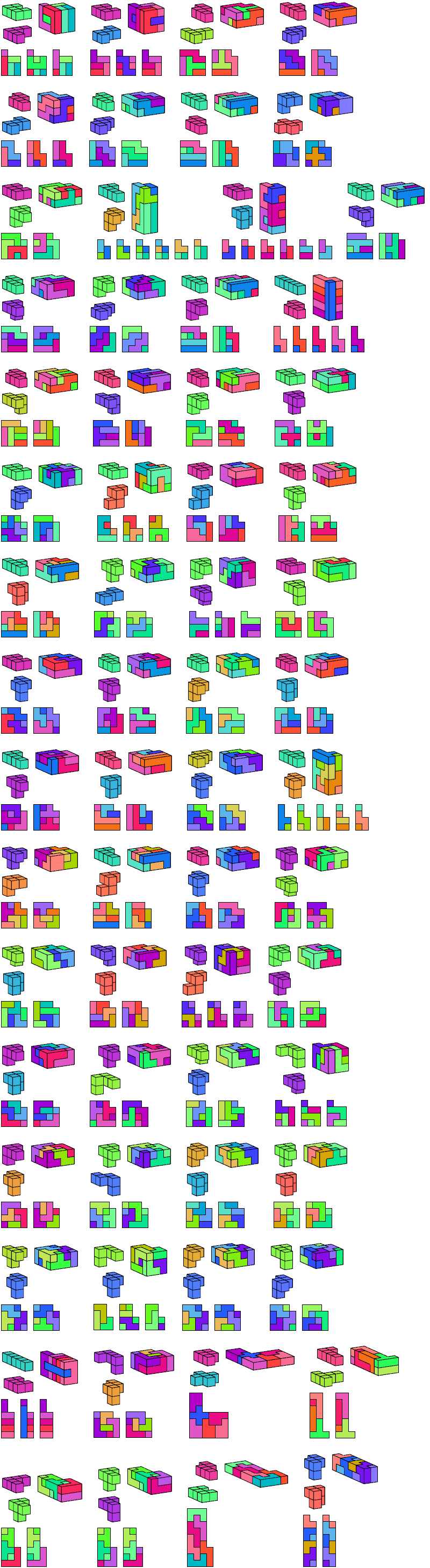
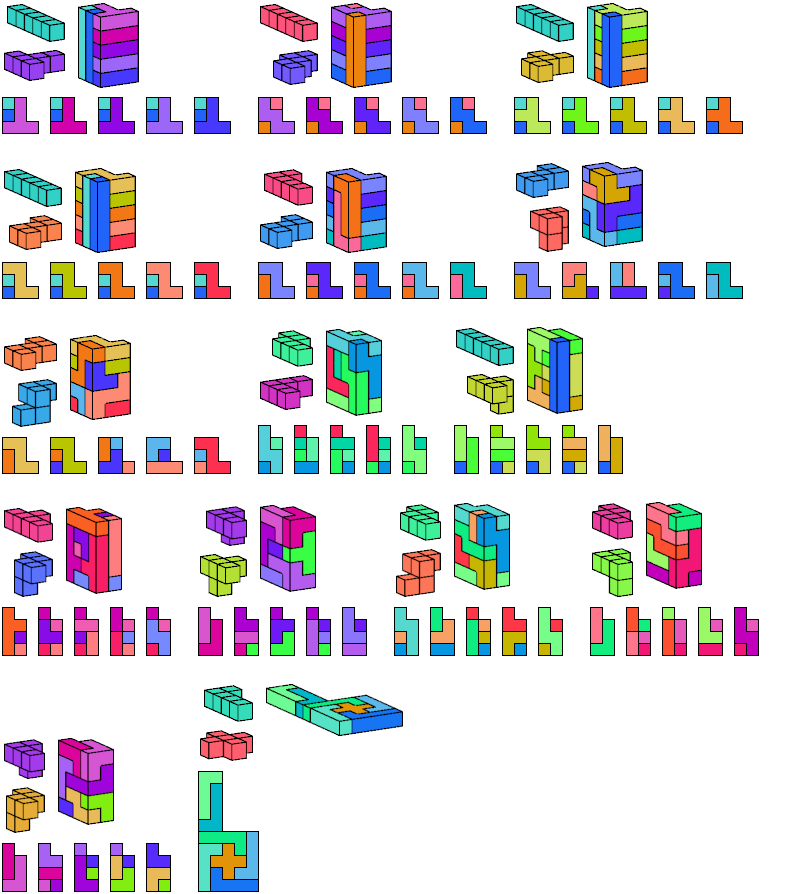
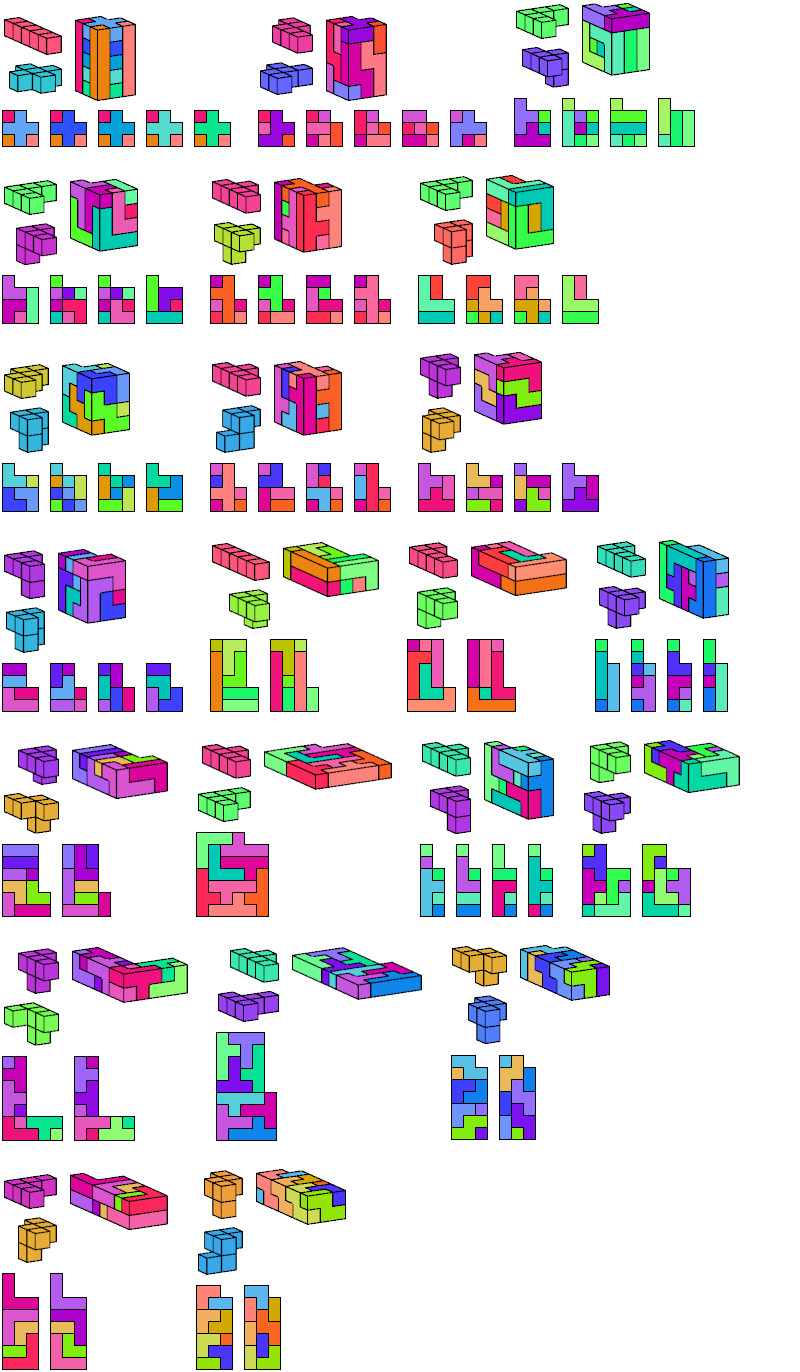
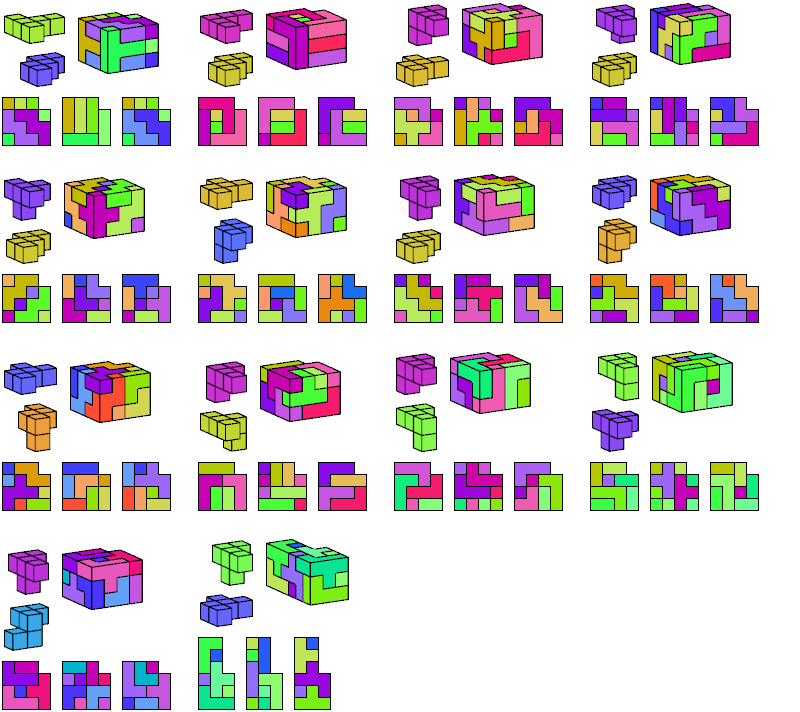
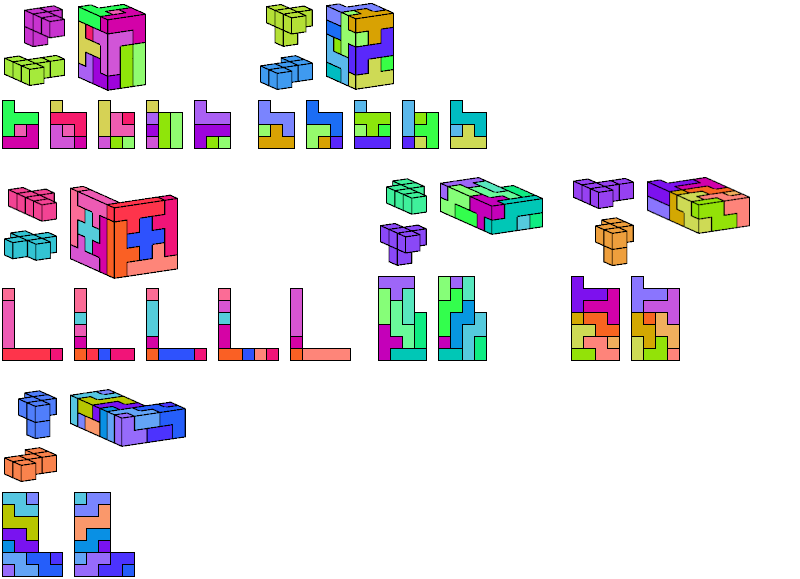
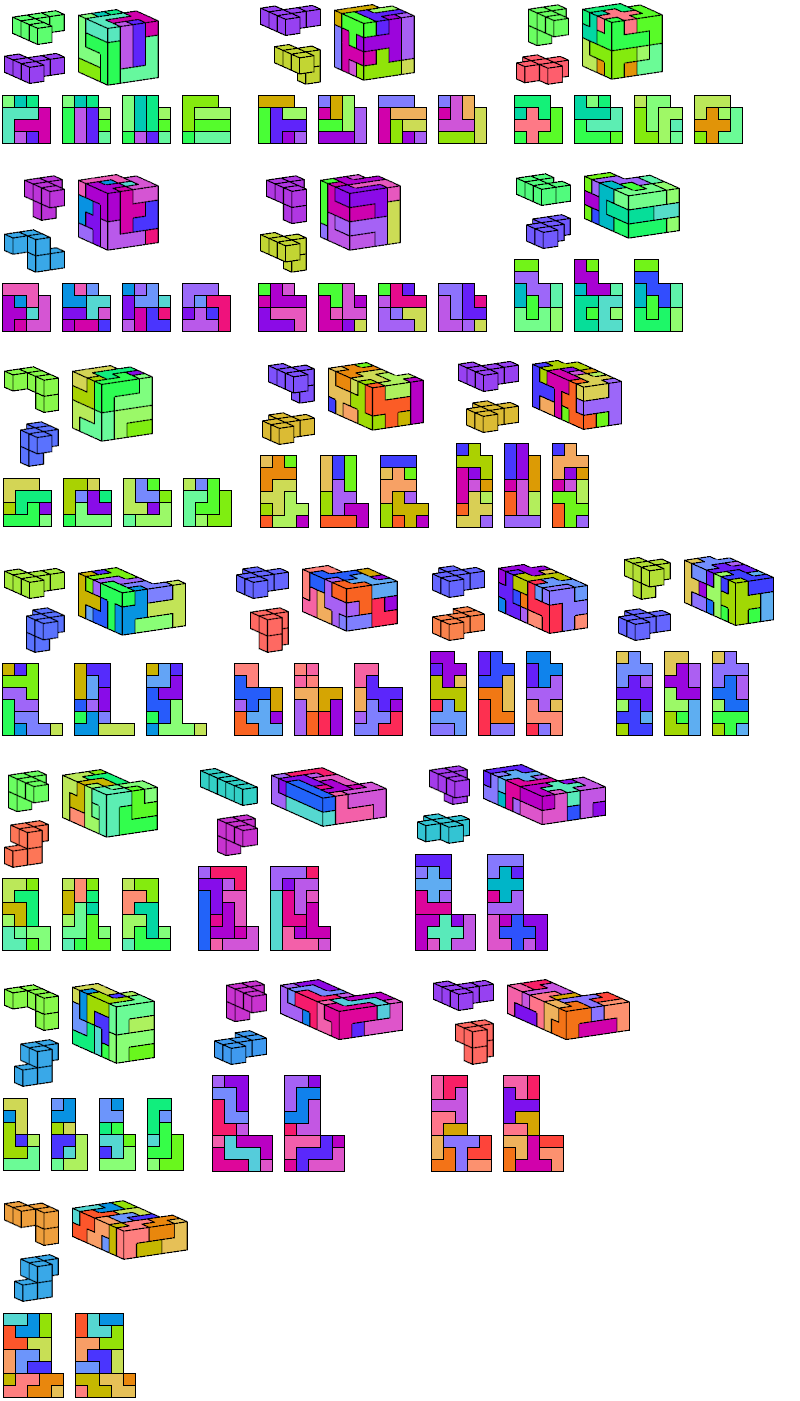
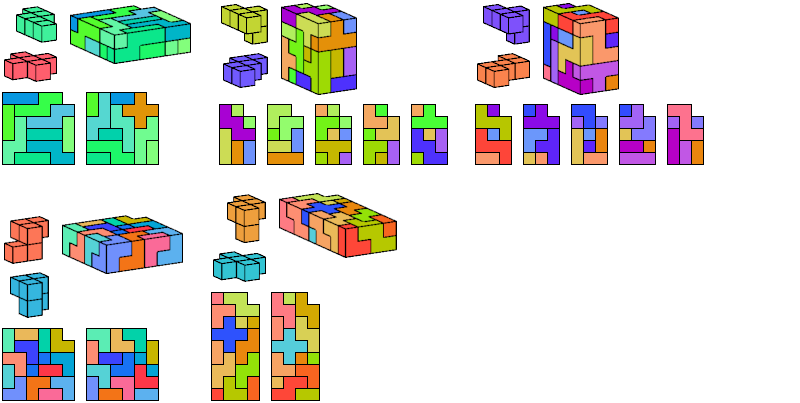
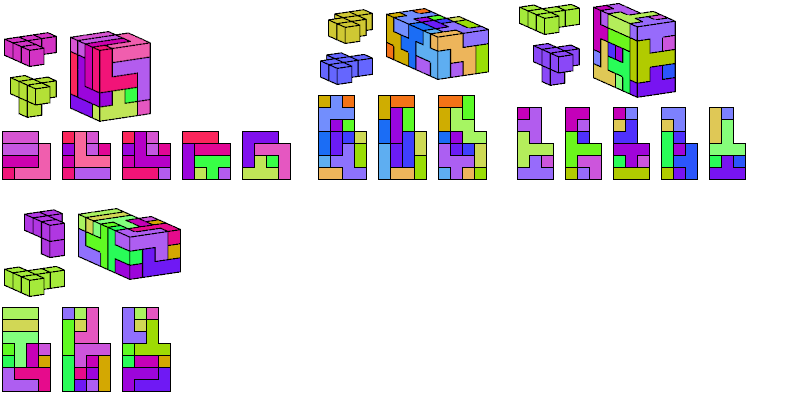
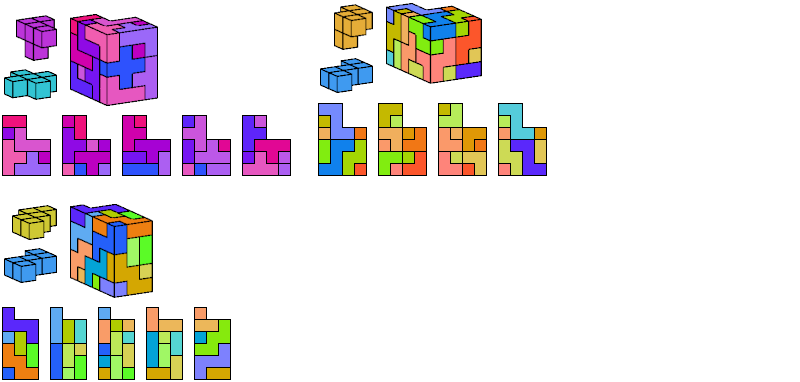
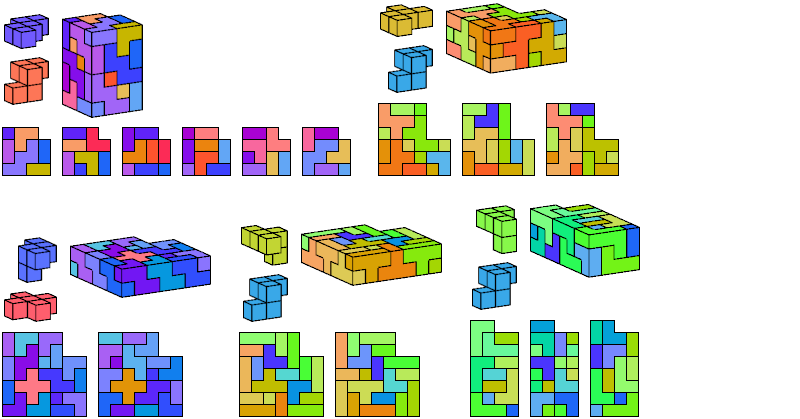
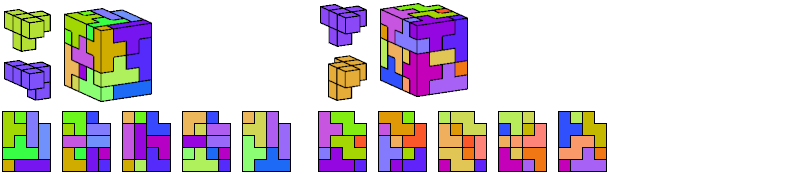
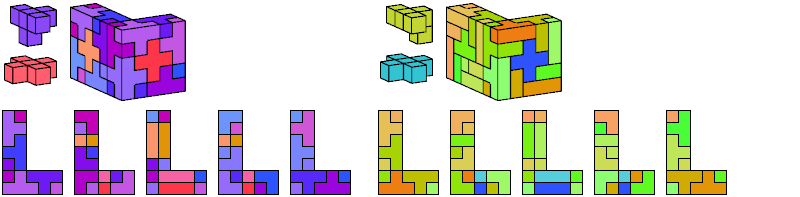
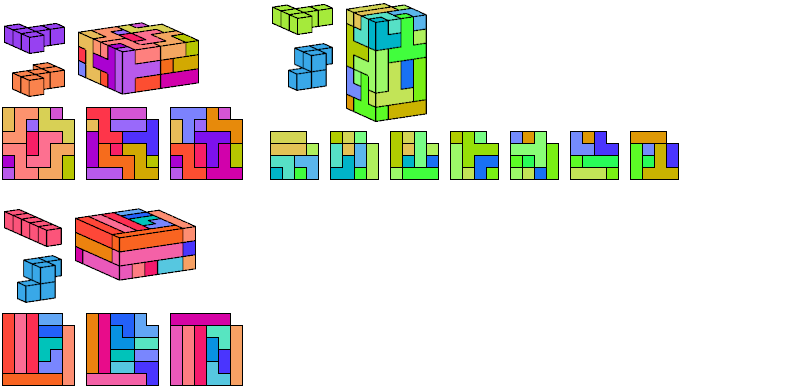
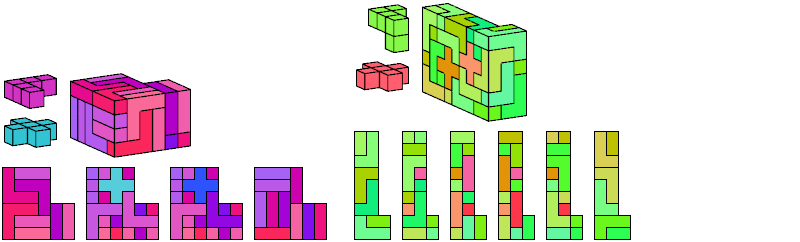
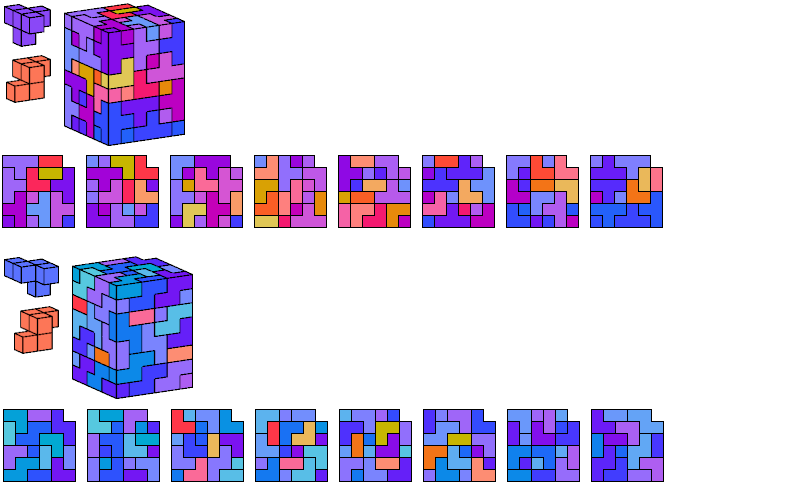
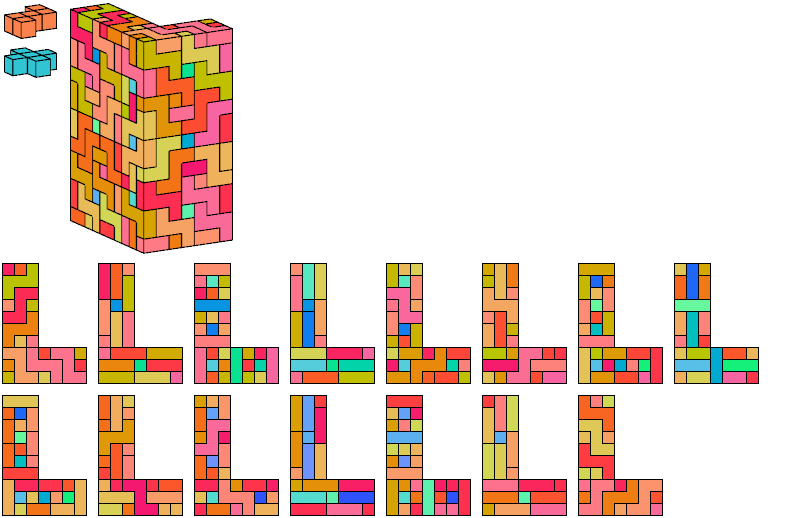
I define an L-shaped polycube as a polycube prism whose base is L-shaped; that is, it consists of a rectangle from one corner of which a smaller rectangle has been excised.
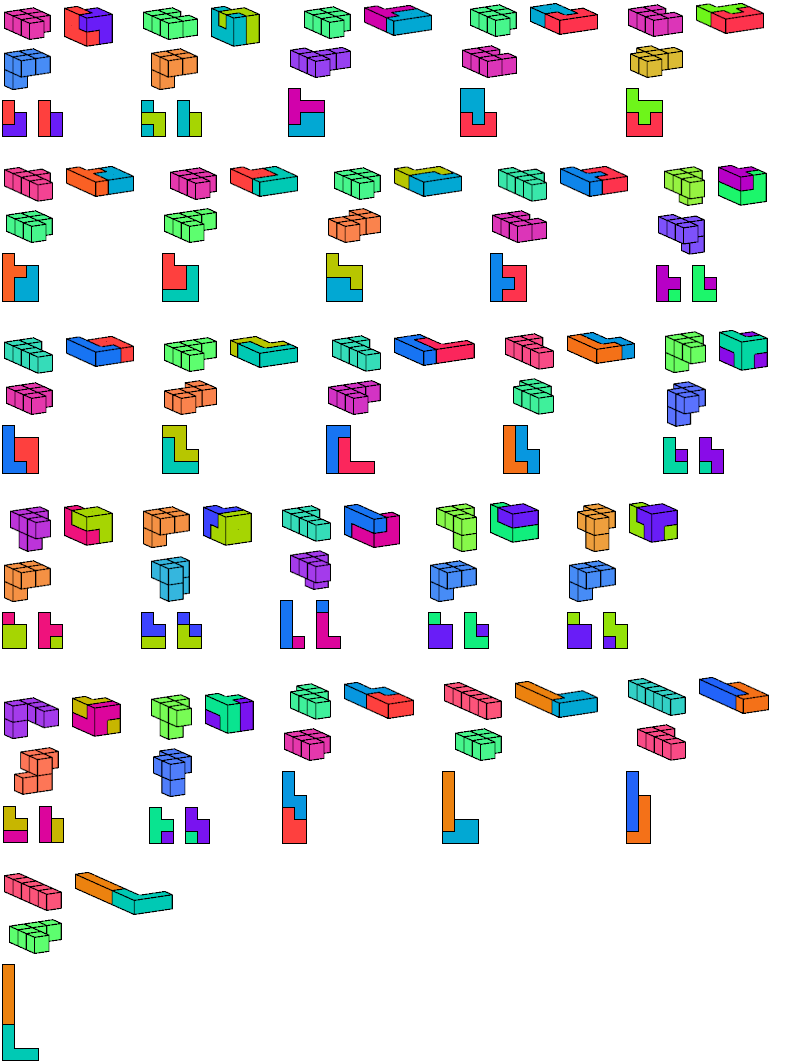
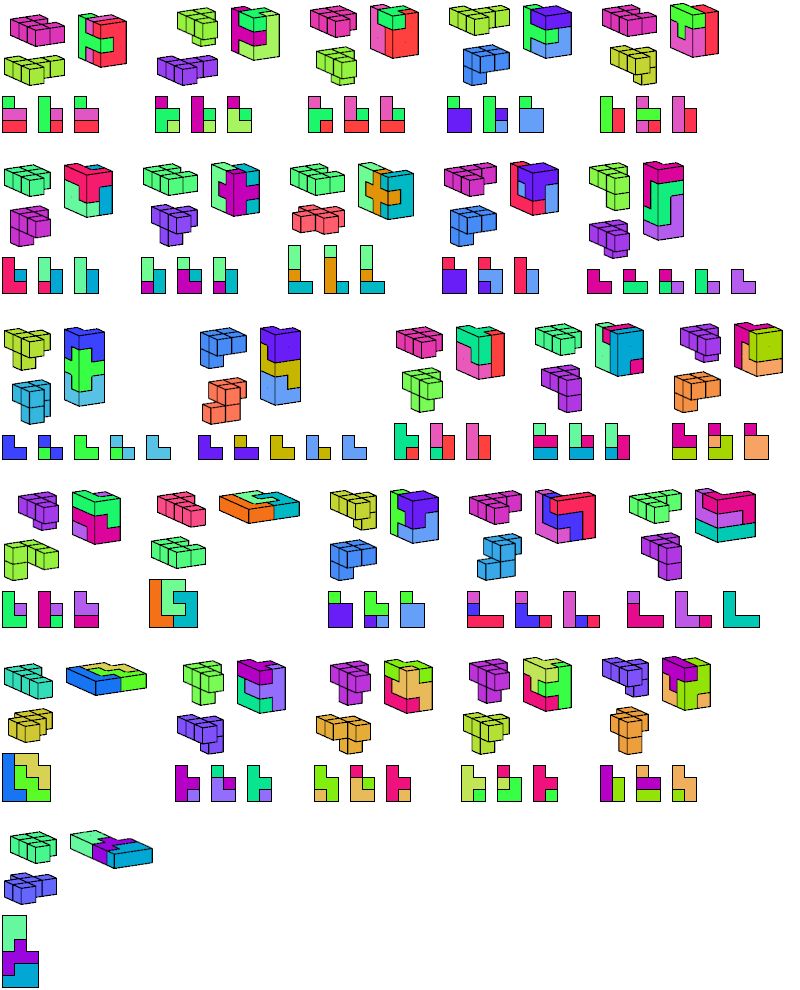
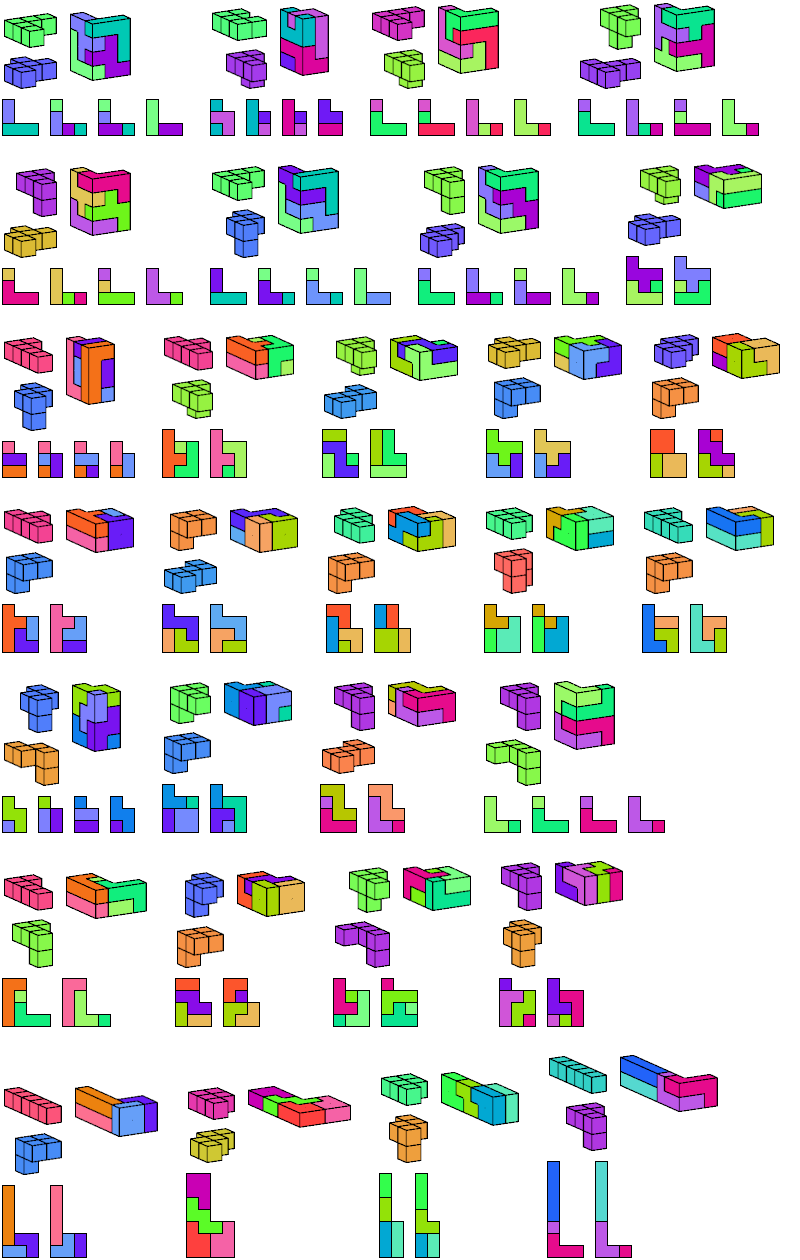
Here I show the smallest known L-shaped polycubes that can be tiled with a given pair of pentacubes, using at least one of each. Chiral pairs of pentacubes are distinguished, and chiral pentacubes may not be reflected when used in these tilings.
If you find a smaller solution, please write.
See also Tiling L Shapes with a Pentacube and L Shapes from Two Pentominoes.
| A | B | E | E′ | F | G | G′ | H | H′ | I | J | J′ | K | L | M | N | P | Q | R | R′ | S | S′ | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 6 | 6 | 12 | 14 | 6 | 13 | 6 | 6 | 6 | 3 | 6 | 4 | 2 | 6 | 8 | 12 | 6 | 8 | 8 | 80 | 6 | 7 | |||||||
| B | 3 | 12 | 18 | 3 | 7 | 2 | 9 | 6 | 19 | 6 | 5 | 3 | 5 | 12 | 12 | 3 | 8 | 14 | 20 | 6 | 14 | ||||||||
| E | 8 | 9 | 9 | 12 | 2 | 6 | 5 | 6 | 6 | 6 | 6 | 3 | 6 | 3 | 2 | 8 | 3 | 6 | 4 | 4 | 6 | 6 | 9 | 16 | 6 | 6 | |||
| F | 18 | 9 | 7 | 4 | 9 | 5 | 12 | 8 | 3 | 4 | 9 | 4 | 12 | 2 | 4 | 15 | 39 | 5 | 12 | ||||||||||
| G | × | 8 | 12 | 21 | 6 | 2 | 12 | 6 | 56 | 7 | 6 | 3 | 30 | 56 | 18 | 12 | 21 | 6 | 3 | 18 | 440 | 8 | 7 | ||||||
| H | 4 | 5 | 6 | 6 | 6 | 4 | 6 | 6 | 4 | 2 | 6 | 8 | 4 | 6 | 10 | 6 | 4 | 6 | 14 | 6 | 10 | ||||||||
| I | 8 | 12 | 2 | 11 | 6 | 2 | 4 | 11 | 4 | 7 | 6 | 2 | 7 | 8 | 5 | 7 | |||||||||||||
| J | 3 | 6 | 2 | 7 | 6 | 3 | 3 | 7 | 8 | 3 | 6 | 3 | 4 | 4 | 9 | 12 | 4 | 4 | |||||||||||
| K | 8 | 8 | 6 | 3 | 4 | 2 | 9 | 10 | 6 | 8 | 6 | 12 | 6 | 12 | |||||||||||||||
| L | 8 | 2 | 2 | 4 | 6 | 4 | 6 | 3 | 2 | 3 | 7 | 5 | 7 | ||||||||||||||||
| M | 10 | 5 | 6 | 19 | 9 | 15 | 3 | 15 | 9 | 20 | 8 | 10 | |||||||||||||||||
| N | 2 | 4 | 6 | 7 | 6 | 6 | 7 | 6 | 14 | 6 | 6 | ||||||||||||||||||
| P | 2 | 5 | 3 | 2 | 2 | 2 | 4 | 6 | 2 | 2 | |||||||||||||||||||
| Q | 4 | 2 | 3 | 2 | 3 | 4 | 6 | 4 | 4 | ||||||||||||||||||||
| R | 30 | 6 | 12 | 12 | 6 | 8 | 9 | 18 | 7 | 16 | |||||||||||||||||||
| S | 4 | 15 | 6 | 3 | 4 | 24 | 8 | 4 | |||||||||||||||||||||
| T | 3 | 12 | 9 | 36 | 8 | 21 | |||||||||||||||||||||||
| U | 6 | 12 | 3 | 2 | 6 | ||||||||||||||||||||||||
| V | 9 | 24 | 8 | 2 | |||||||||||||||||||||||||
| W | 28 | 6 | 16 | ||||||||||||||||||||||||||
| X | 10 | 126 | |||||||||||||||||||||||||||
| Y | 5 | ||||||||||||||||||||||||||||
| Z | |||||||||||||||||||||||||||||



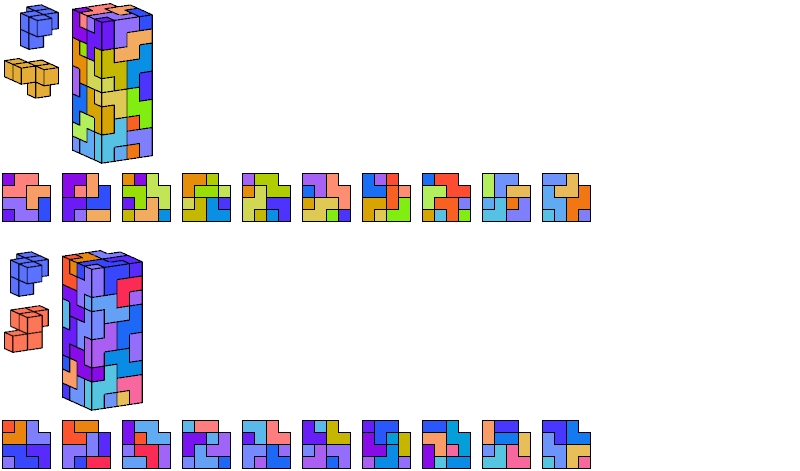

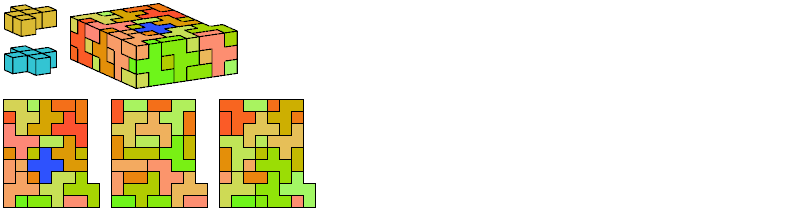
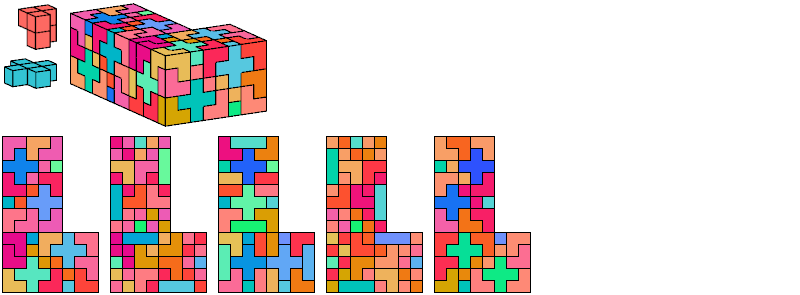
Last revised 2024-02-07.