Pentacube Pair Odd Boxes

Introduction

A pentacube is a solid made of 5 equal cubes joined face to face. There are 29 pentacubes, distinguishing mirror images.

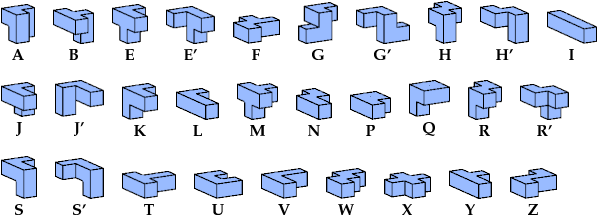
I indicate mirror images with a prime mark (′). For example, S′ denotes the mirror image of pentacube S.

All but two of the pentacubes, G and X, can tile a rectangular prism, or box. A box is odd if it has an odd number of cells. Such a box must have all its dimensions odd.

Here I show the smallest odd box known to be tilable with each pair of pentacubes, using at least one copy of each of the two pentacubes. If you find a solution smaller than one shown, or solve an unsolved case, please write.

See also Pentacube Pair Boxes.

Tile Counts

Click on an entry in the table to see the corresponding tiling.

  ABEE′FGG′HH′IJJ′KLMNPQRR′SS′TUVWXYZ
A 25915?45211515152515945?1515151521?1515
B  152149451591515351591525211591521491521
E   151515211515999999159991591515999211515
F    2115915157211591521152199216359
G      ×45?271592115?21945??332127151533?1539
H        4599999211594545451515151599351515
I       1521315153915219979979
J           999159999159999992199
K         152115991527219159151515
L          157399159999599
M           21915?152192121×1521
N            91521151591521252115
P             9993939533
Q              4599159915159
R                   45212115915211171515
S                     2721152121151515
T                 9152155925
U                  9213119
V                   2149153
W                    571515
X                     563
Y                      5
Z                       

Impossible Cases

G and G′ cannot tile even one edge of a box, much less a whole box.

M and X, colored like a 3D checkerboard, have four cells of one color and one of the other. Thus an odd number of M and X pentacubes have a net color imbalance that is an odd multiple of 3. Every odd box has a color imbalance of 1.

Last revised 2024-02-05.

Back to Polyform Tiling < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]