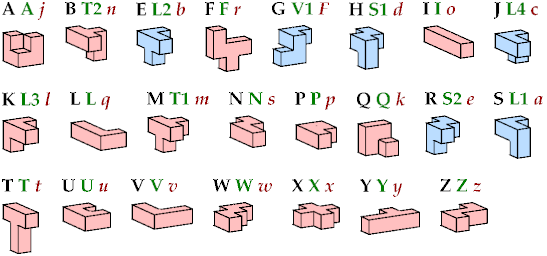

The six blue tiles have distinct mirror images. Kate Jones's systematic names are shown in green. Donald Knuth's names are shown in red. In all three nomenclatures, pentacubes that lie all in one plane are named for the corresponding pentominoes. (Kate Jones uses Solomon Golomb's names; Donald Knuth uses John Conway's names.)
Can a rectangular prism, or box, be filled with copies of a pentacube? For each pentacube, here is the smallest known box that it can fill. Some pentacubes have other solutions with the same volume and different dimensions. Torsten Sillke's polycube box tiling page identifies many boxes besides the smallest that can be tiled by polycubes. Toshihiro Shirakawa's Box Packing Collection has extensive box tiling data for polycubes, edge-polycubes, and polyhypercubes.
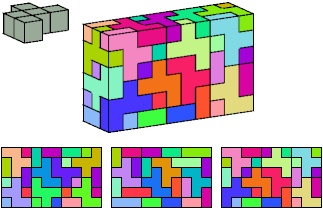
Most of these constructions are taken from the text representations in Michael Reid's Box Collection. Most of these solutions are Mike's. In his collection you can also find solutions for polycubes of other sizes.
Neither the G nor the X pentacube can tile a box. See below for hybrid solutions.
See also Pentacubes in an Odd Box.
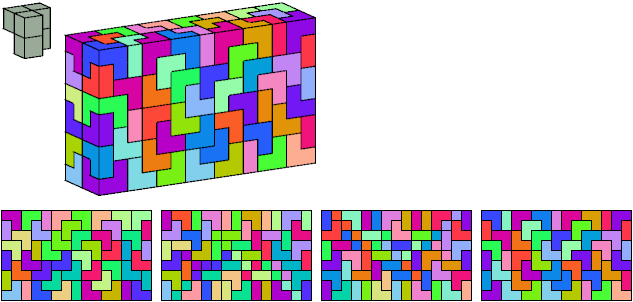
Toshihiro Shirakawa (白川俊博) (2014)
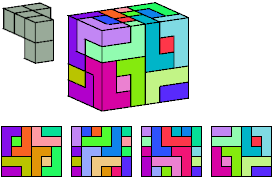
This was the first solution found:
144 tiles, 4×9×20
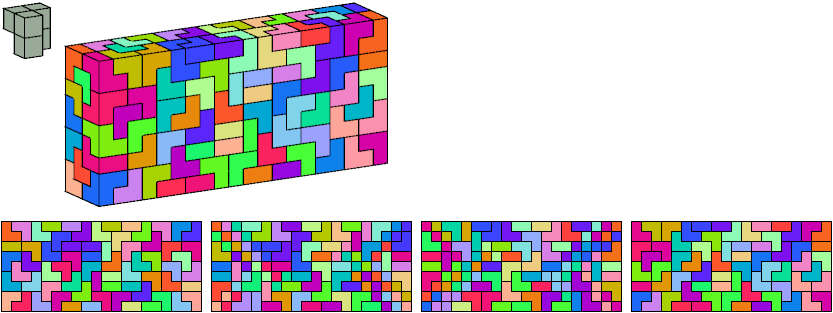
Helmut Postl
This pentacube also tiles a 6×10×10 box (120 tiles) and an 8×8×10 box (128 tiles).
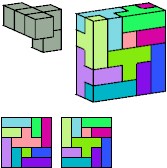
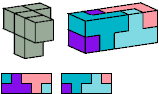
Primes: 2×2×5, 3×4×5, 3×5×5,
3×5×6, 2×5×7, 3×5×7,
2×3×10, 3×3×10, 3×3×15.
Without reflection:
2×2×5,
4×5×5,
5×5×5,
3×5×6,
5×5×7,
3×5×8,
3×5×9,
3×5×10,
3×5×11,
3×5×13.
Patrick Hamlyn
See below for hybrid solutions.
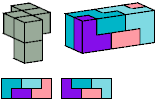
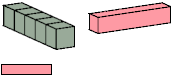
Primes: 1×1×5.
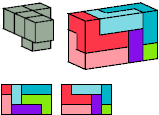
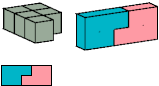
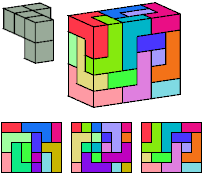
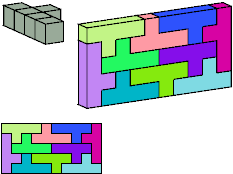
Without reflection: 12 tiles, 3×4×5
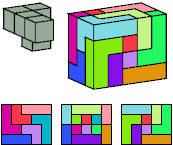
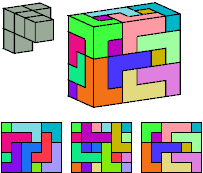
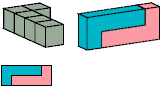
Primes: 1×2×5, 3×5×5, 1×7×15.

Toshihiro Shirakawa (白川俊博) (2014)
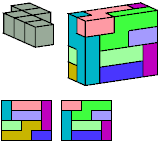
Primes: 1×2×5, 3×3×5, 1×7×15.
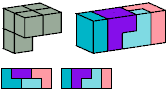
Patrick Hamlyn
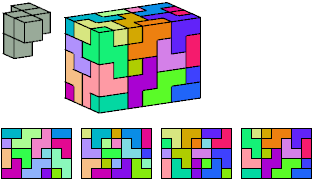
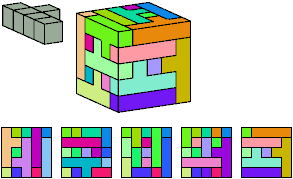
Without reflection: 64 tiles, 5×8×8
Helmut Postl
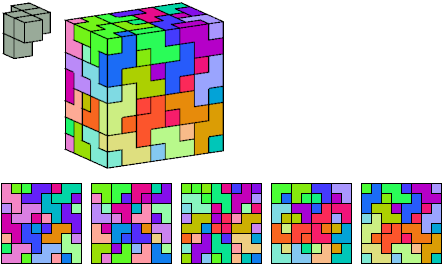
Patrick Hamlyn
Without reflections: 24 tiles, 4×5×6
Patrick Hamlyn

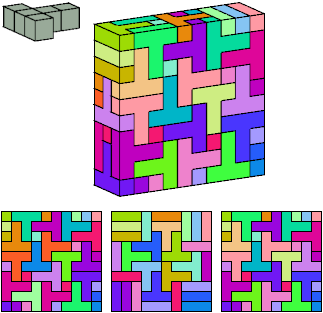
Frits Göbel

Toshihiro Shirakawa (白川俊博)
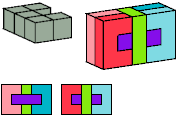

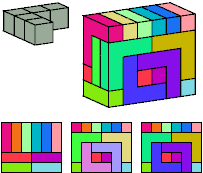

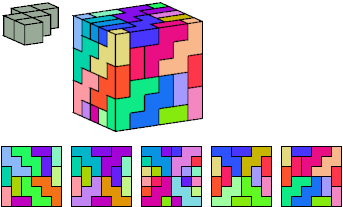
Torsten Sillke


See below for hybrid solutions.
David Klarner
Wolf

Toshihiro Shirakawa (白川俊博)
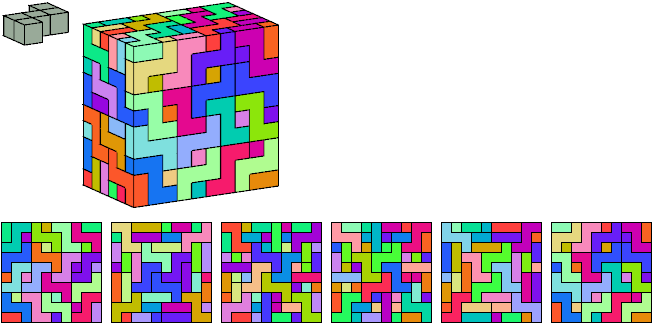
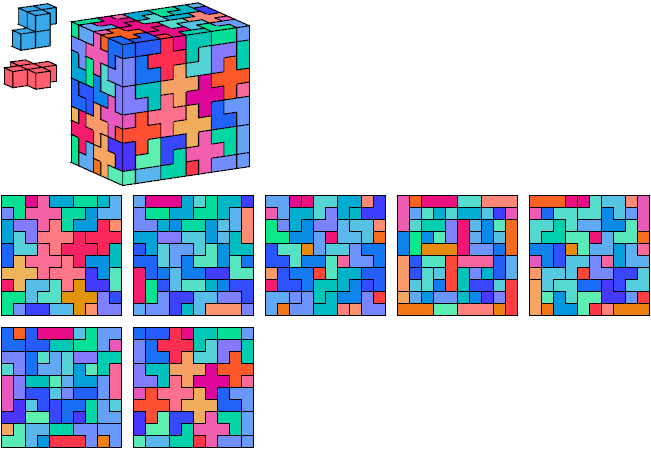
With reflection: 100 G tiles, 40 X tiles, 7×10×10.
George Sicherman
Without reflection: 128 G tiles, 72 X tiles, 10×10×10.
George Sicherman
The unreflected G and X pentacubes can also tile a 10×10×12 box, a 10×10×13 box, a 10×10×14 box, and a 10×10×15 box.
Last revised 2023-06-16.