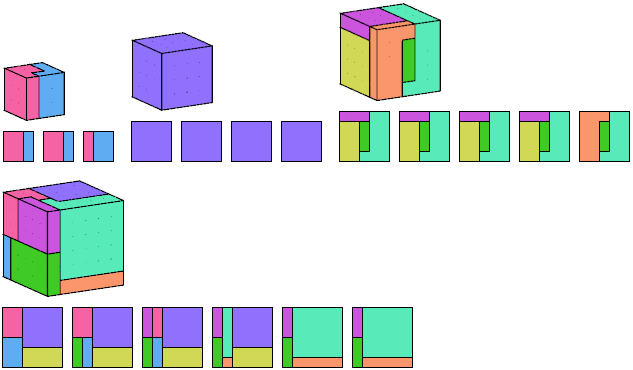
This dissection by Noam D. Elkies uses 8 pieces:

According to Elkies, it was JHI
(identity unknown,
perhaps connected with the Jeremiah Horrocks Institute) who first
showed that 8 pieces are necessary.
The proof is simple: the 6×6×6 cube has 8 corner cells.
Any piece big enough to include two of the corner cells will be too big
to fit in a smaller cube.
Therefore each of the 8 corners of the 6×6×6 cube
must belong to a separate piece.
The earliest 8-piece dissection known to Elkies appears in Harry Lindgren's Geometric Dissections (1981). The book attributes it to R. F. Wheeler. It is more complicated than Elkies's.
It is not known how many of the pieces in an 8-piece dissection can be rectangular prisms. However, T. H. O'Beirne found a dissection with 9 pieces, all rectangular prisms. See Martin Gardner's Knotted Doughnuts and Other Mathematical Entertainments (1986).
Edo Timmermans analyzed the problem and found a solution in which no pieces are rotated. See this page of Greg Frederickson's.
Last revised 2021-06-05.