

The term irreptile was coined by Dr. Karl Scherer, who studied such tilings extensively. His results appear in chapters 3 and 4 of his book A Puzzling Journey to the Reptiles and Related Animals, and in some of his Wolfram Demonstrations, notably Irreptiles and Some Irreptiles of Order Greater Than 20.
Erich Friedman's Math Magic for October 2002 presents irreptilings for various kinds of polyforms, discovered by Scherer, Friedman, and others. It shows minimal known polyabolo irreptilings for polyaboloes with up to seven cells.
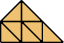
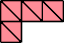
Here I present minimal known irreptilings for polyaboloes, including all those that Dr. Scherer showed to have irreptilings. Polyaboloes with the same shapes as smaller polyaboloes are omitted. Proper reptilings are shown in bright green. Tiles with shaded backgrounds are polyominoes.

|  |
| 2 |

|  |
| 4 | |

|  |
| 2 |

| 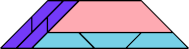 |
| 8 | |

|  Karl Scherer |
| 3 |

|  |
| 4 | |

| 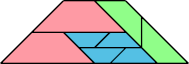 Karl Scherer |
| 8 | |
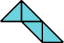
| 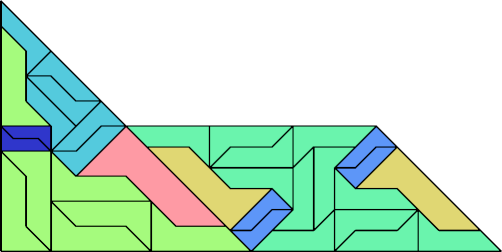 |
| 34 | |

|  |
| 4 |

| 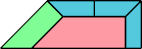 Karl Scherer |
| 5 | |
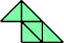
| 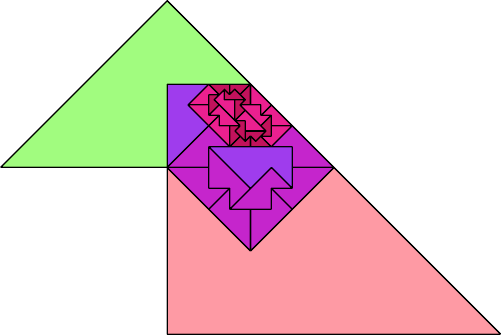 Karl Scherer |
| 34 | |
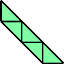
|  |
| 14 |

|  |
| 4 | |

|  |
| 4 | |

| 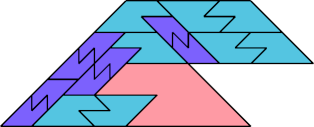 |
| 17 | |

|  |
| 4 | |

| 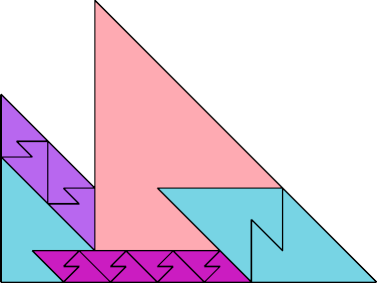 |
| 16 | |

| 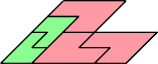 |
| 5 | |
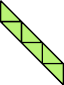
|  |
| 4 | |

| 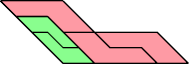 |
| 5 | |
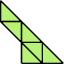
| 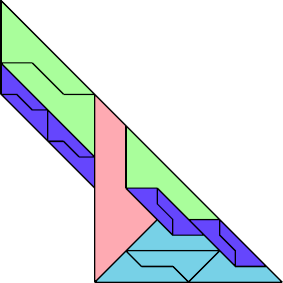 |
| 16 | |

| 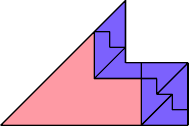 Karl Scherer |
| 8 |

| 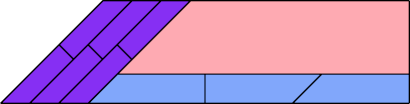 |
| 10 | |
| 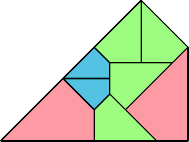 |
| 8 | |

|  |
| 18 |
|  |
| 4 | |
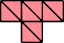
| 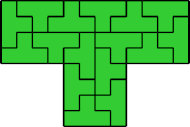 |
| 16 | |

|  |
| 4 | |
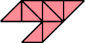
| 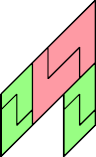 |
| 6 | |

| 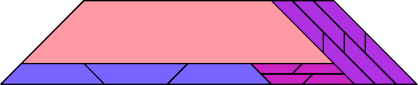 |
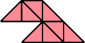
| 14 | |
| 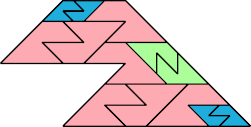 |
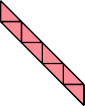
| 13 | |
|  |
| 4 | |
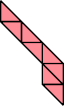
| 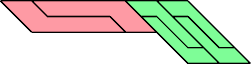 |
| 6 | |
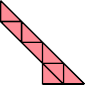
| 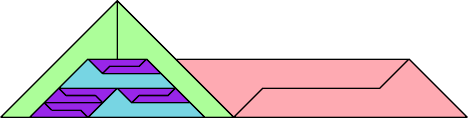 Karl Scherer |
| 14 | |
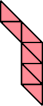
| 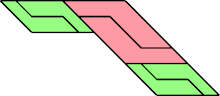 |
| 6 | |
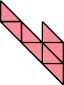
| 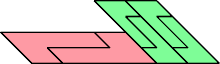 |
| 6 | |
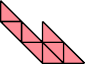
| 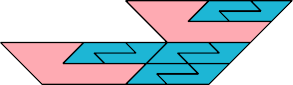 |
| 10 | |
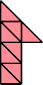
| 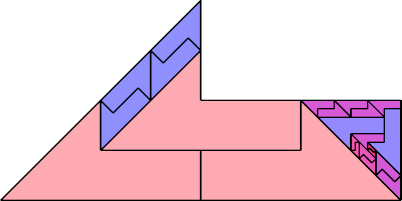 |
| 23 | |
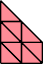
| 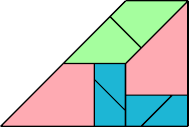 |
| 8 |

| 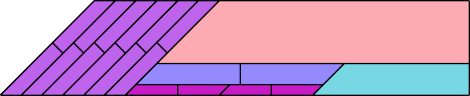 |
| 20 | |

|  |
| 21 |

|  |
| 4 | |

| 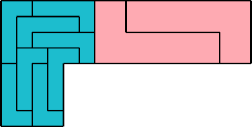 Karl Scherer |
| 10 | |

| 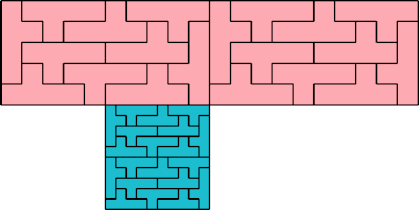 Karl Scherer |
| 40 | |

|  |
| 4 | |

|  |
| 4 | |

|  |
| 4 | |

| 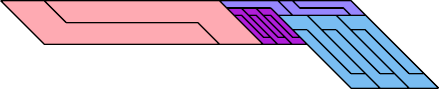 |
| 17 | |
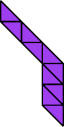
| 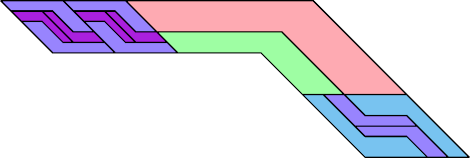 |
| 14 | |

| 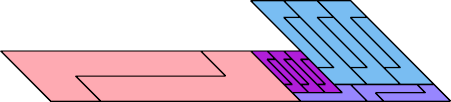 |
| 17 | |
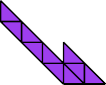
| 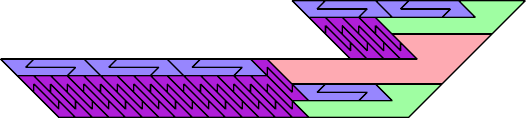 |
| 55 | |

| 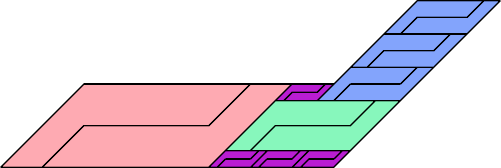 |
| 18 | |
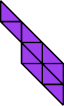
| 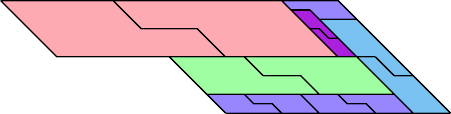 |
| 13 | |
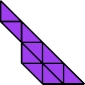
| 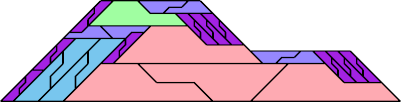 |
| 35 | |

| 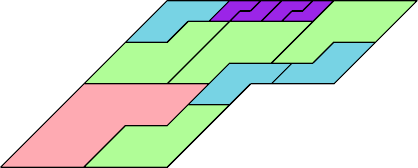 |
| 12 | |

| 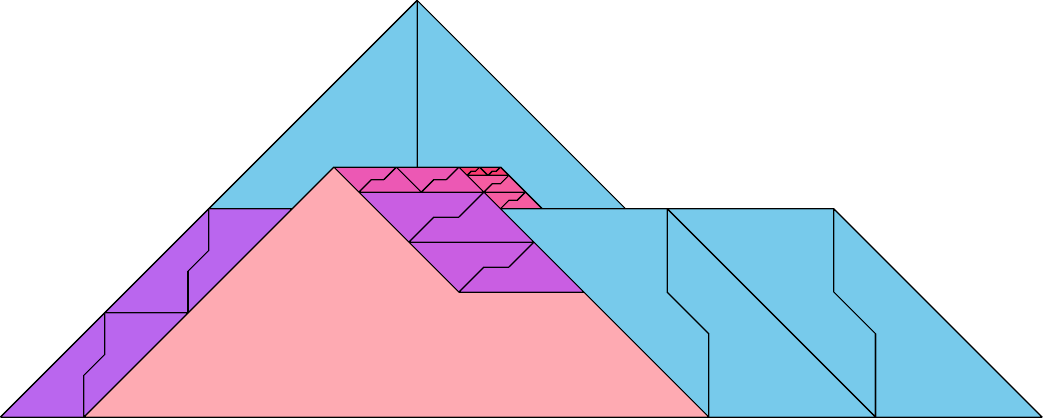 Karl Scherer |
| 27 | |

| 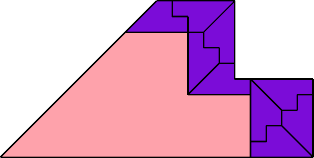 |
| 10 |
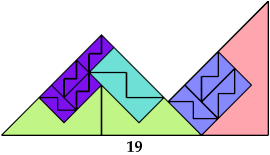
This 16-bolo irreptiling by Dr. Scherer has 19 tiles. The book and demo state that it has 21.
Last revised 2018-09-07.