
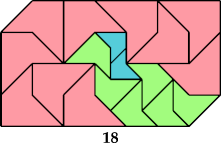
How few similar (scaled) copies of a given polyabolo can form a convex shape? For most polyaboloes, the tilings with the fewest tiles use equal tiles, as with this triabolo:

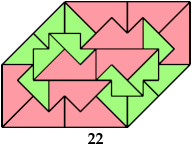
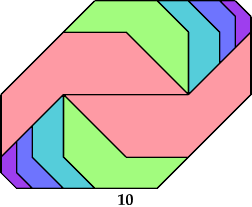
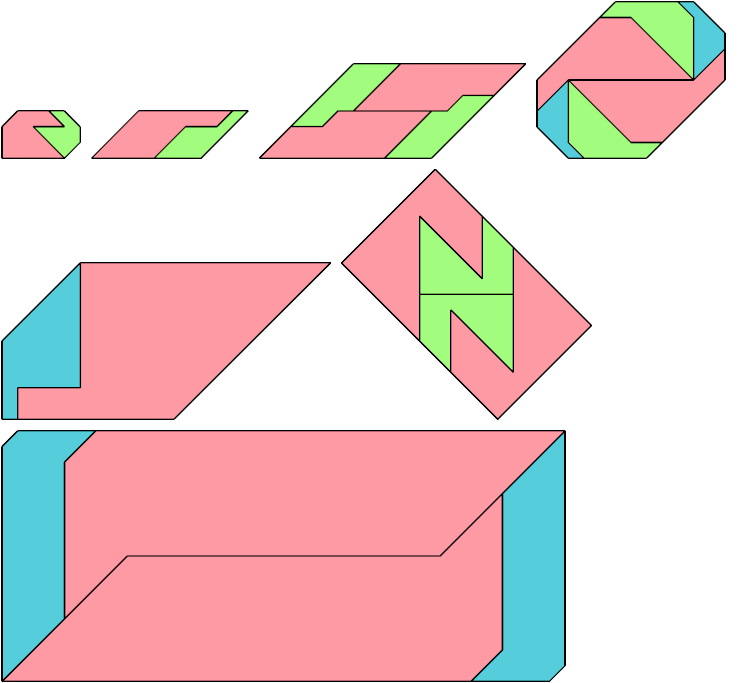
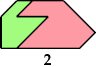
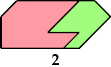
Here I show the only polyaboloes I know of for which the convex tiling with the fewest tiles uses tiles of different sizes. If you find a tiling with fewer tiles than shown, please write.
So far as I know, these polyaboloes cannot tile any convex shape at a uniform scale.
Andrew Bayly points out that polyominoes are also polyaboloes, and that some polyominoes have this property. I do not consider polyominoes here.
See also Similar Polyaboloes Tiling a Triangle, Similar Polyaboloes Tiling a Square, Similar Polyaboloes Tiling an Octagon, and Similar Polyiamonds Forming a Convex Shape.
Last revised 2025-04-20.