
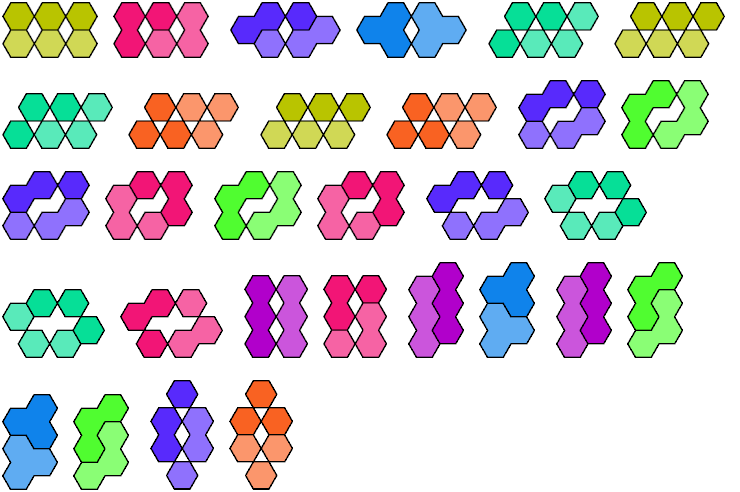
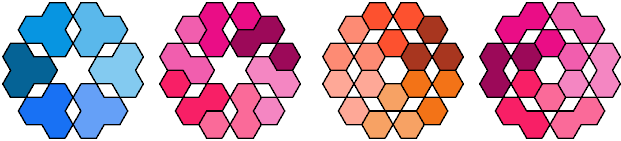
The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Here are minimal known compatibility figures for pairs of trihings.

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | * | 3 | 2 | × | 2 | 3 | × | 2 |
| 2 | 3 | * | 2 | 2 | 2 | 3 | 2 | 2 |
| 3 | 2 | 2 | * | × | 2 | × | × | 6 |
| 4 | × | 2 | × | * | × | 2 | 2 | 2 |
| 5 | 2 | 2 | 2 | × | * | × | × | 2 |
| 6 | 3 | 3 | × | 2 | × | * | 2 | 2 |
| 7 | × | 2 | × | 2 | × | 2 | * | 6 |
| 8 | 2 | 2 | 6 | 2 | 2 | 2 | 6 | * |

Last revised 2014-12-08.