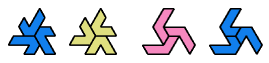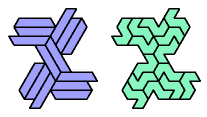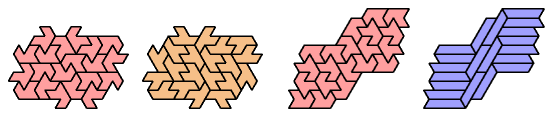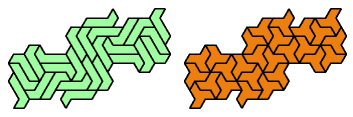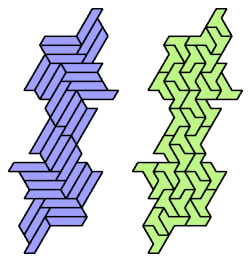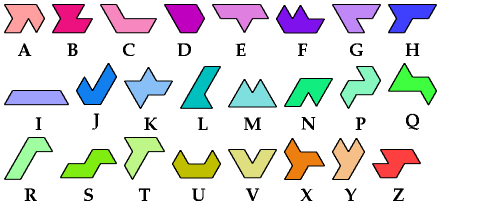
Dr. Erich Friedman's Math Magic for September 2004 shows compatibility figures for polyiamonds up to order 6 (and many other polyforms). Here I present the smallest known compatibility figures for heptiamonds.

| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 2 | 3 | 3 | 2 | 3 | 2 | 3 | 10 | 3 | 2 | 3 | 6 | 3 | 3 | 3 | 2 | 2 | 3 | 6 | 3 | 6 | 6 | 3 |
| B | 2 | * | 3 | 6 | 2 | 3 | 2 | 2 | 2 | 6 | 2 | 2 | 2 | 3 | 18 | 3 | 3 | 2 | 2 | ? | ? | 6 | 3 | 3 |
| C | 3 | 3 | * | 3 | 3 | 2 | 3 | 3 | 2 | 2 | ? | 2 | 6 | 2 | 4 | 3 | 2 | 3 | 2 | 2 | 2 | 4 | 2 | 3 |
| D | 3 | 6 | 3 | * | 3 | 3 | 3 | 6 | 2 | 2 | ? | 3 | 6 | 3 | 3 | 3 | 2 | 3 | 6 | 3 | 3 | 6 | 6 | 3 |
| E | 2 | 2 | 3 | 3 | * | 2 | 3 | 2 | 2 | 6 | 2 | 3 | 6 | 6 | 3 | 3 | 3 | 2 | 3 | 3 | 3 | 3 | 2 | 2 |
| F | 3 | 3 | 2 | 3 | 2 | * | 2 | 6 | 3 | 2 | 3 | 3 | 6 | 3 | 2 | 6 | 2 | 6 | 2 | 3 | ? | ? | 2 | 3 |
| G | 2 | 2 | 3 | 3 | 3 | 2 | * | 2 | 2 | 2 | 6 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 2 | ? | 3 | 12 | 2 | 4 |
| H | 3 | 2 | 3 | 6 | 2 | 6 | 2 | * | 2 | 6 | 2 | 3 | 2 | 6 | 2 | 2 | 3 | 2 | 3 | 2 | ? | 2 | 6 | 2 |
| I | 10 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | * | 2 | ? | 2 | 9 | 2 | 9 | 9 | 2 | 2 | 4 | 4 | 4 | ? | 2 | 2 |
| J | 3 | 6 | 2 | 2 | 6 | 2 | 2 | 6 | 2 | * | 3 | 6 | ? | 3 | 2 | 2 | 2 | 4 | 3 | 2 | 2 | ? | 2 | 2 |
| K | 2 | 2 | ? | ? | 2 | 3 | 6 | 2 | ? | 3 | * | 3 | 6 | 3 | 6 | 3 | 6 | 2 | 3 | 3 | ? | 3 | 3 | 6 |
| L | 3 | 2 | 2 | 3 | 3 | 3 | 2 | 3 | 2 | 6 | 3 | * | 2 | 2 | 54 | 2 | 3 | 3 | 2 | 3 | 12 | ? | 6 | 4 |
| M | 6 | 2 | 6 | 6 | 6 | 6 | 2 | 2 | 9 | ? | 6 | 2 | * | 2 | ? | 2 | 12 | 18 | 6 | ? | ? | ? | 6 | 2 |
| N | 3 | 3 | 2 | 3 | 6 | 3 | 2 | 6 | 2 | 3 | 3 | 2 | 2 | * | 3 | 3 | 3 | 3 | 3 | ? | 2 | ? | 6 | 2 |
| P | 3 | 18 | 4 | 3 | 3 | 2 | 2 | 2 | 9 | 2 | 6 | 54 | ? | 3 | * | 3 | 6 | 2 | 6 | 3 | 3 | 2 | 2 | 2 |
| Q | 3 | 3 | 3 | 3 | 3 | 6 | 2 | 2 | 9 | 2 | 3 | 2 | 2 | 3 | 3 | * | 2 | 2 | 3 | 4 | ? | 18 | 6 | 2 |
| R | 2 | 3 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 2 | 6 | 3 | 12 | 3 | 6 | 2 | * | 2 | 2 | 3 | 3 | 6 | 2 | 6 |
| S | 2 | 2 | 3 | 3 | 2 | 6 | 3 | 2 | 2 | 4 | 2 | 3 | 18 | 3 | 2 | 2 | 2 | * | 3 | 4 | 6 | 2 | 2 | 2 |
| T | 3 | 2 | 2 | 6 | 3 | 2 | 2 | 3 | 4 | 3 | 3 | 2 | 6 | 3 | 6 | 3 | 2 | 3 | * | 6 | 18 | 6 | 2 | 3 |
| U | 6 | ? | 2 | 3 | 3 | 3 | ? | 2 | 4 | 2 | 3 | 3 | ? | ? | 3 | 4 | 3 | 4 | 6 | * | 2 | 3 | 6 | 6 |
| V | 3 | ? | 2 | 3 | 3 | ? | 3 | ? | 4 | 2 | ? | 12 | ? | 2 | 3 | ? | 3 | 6 | 18 | 2 | * | 6 | 6 | 3 |
| X | 6 | 6 | 4 | 6 | 3 | ? | 12 | 2 | ? | ? | 3 | ? | ? | ? | 2 | 18 | 6 | 2 | 6 | 3 | 6 | * | 3 | 2 |
| Y | 6 | 3 | 2 | 6 | 2 | 2 | 2 | 6 | 2 | 2 | 3 | 6 | 6 | 6 | 2 | 6 | 2 | 2 | 2 | 6 | 6 | 3 | * | 2 |
| Z | 3 | 3 | 3 | 3 | 2 | 3 | 4 | 2 | 2 | 2 | 6 | 4 | 2 | 2 | 2 | 2 | 6 | 2 | 3 | 6 | 3 | 2 | 2 | * |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | X | Y | Z |



| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 2 | 9 | 3 | 2 | 3 | 2 | 3 | 20 | ? | 2 | ? | ? | 3 | 3 | 6 | 2 | 2 | 6 | 6 | 3 | 6 | 20 | 3 |
| B | 2 | * | 10 | ? | 2 | 28 | 2 | 2 | 2 | ? | 2 | 2 | 2 | 22 | ? | 6 | 12 | 2 | 2 | ? | ? | ? | 8 | 4 |
| C | 9 | 10 | * | 3 | 4 | 2 | 3 | 6 | 2 | 3 | ? | 2 | 6 | 2 | 4 | 3 | 2 | 3 | 2 | 6 | 2 | 4 | 2 | 6 |
| D | 3 | ? | 3 | * | ? | 4 | 3 | 6 | 2 | 2 | ? | ? | ? | 3 | 3 | 3 | 2 | 3 | 6 | 4 | 3 | 6 | 6 | 3 |
| E | 2 | 2 | 4 | ? | * | 2 | ? | 2 | 2 | ? | 2 | 4 | ? | 12 | 6 | ? | 4 | 2 | 3 | ? | ? | 12 | 2 | 2 |
| F | 3 | 28 | 2 | 4 | 2 | * | 2 | ? | 3 | 2 | ? | ? | ? | 4 | 2 | 6 | 2 | 9 | 2 | 4 | ? | ? | 2 | 3 |
| G | 2 | 2 | 3 | 3 | ? | 2 | * | 2 | 2 | 2 | ? | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 2 | ? | ? | ? | 2 | 4 |
| H | 3 | 2 | 6 | 6 | 2 | ? | 2 | * | 2 | ? | 2 | 2 | 2 | 6 | 2 | 2 | 4 | 2 | 6 | 2 | ? | 2 | 28 | 2 |
| I | 20 | 2 | 2 | 2 | 2 | 3 | 2 | 2 | * | 2 | ? | 2 | ? | 2 | 14 | ? | 2 | 2 | 36 | 4 | ? | ? | 2 | 2 |
| J | ? | ? | 3 | 2 | ? | 2 | 2 | ? | 2 | * | ? | ? | ? | ? | 2 | 2 | 2 | 16 | ? | 4 | 3 | ? | 2 | 2 |
| K | 2 | 2 | ? | ? | 2 | ? | ? | 2 | ? | ? | * | ? | 6 | ? | 6 | 4 | ? | 2 | 4 | ? | ? | ? | ? | ? |
| L | ? | 2 | 2 | ? | 4 | ? | 2 | 2 | 2 | ? | ? | * | 2 | 2 | ? | 2 | 4 | 6 | 2 | ? | ? | ? | ? | 10 |
| M | ? | 2 | 6 | ? | ? | ? | 2 | 2 | ? | ? | 6 | 2 | * | 2 | ? | 2 | ? | ? | ? | ? | ? | ? | ? | 2 |
| N | 3 | 22 | 2 | 3 | 12 | 4 | 2 | 6 | 2 | ? | ? | 2 | 2 | * | 3 | 3 | 6 | 3 | ? | ? | 2 | ? | ? | 2 |
| P | 3 | ? | 4 | 3 | 6 | 2 | 2 | 2 | 14 | 2 | 6 | ? | ? | 3 | * | 4 | 6 | 2 | 6 | 3 | 3 | 2 | 2 | 2 |
| Q | 6 | 6 | 3 | 3 | ? | 6 | 2 | 2 | ? | 2 | 4 | 2 | 2 | 3 | 4 | * | 2 | 2 | 4 | 4 | ? | ? | 10 | 2 |
| R | 2 | 12 | 2 | 2 | 4 | 2 | 2 | 4 | 2 | 2 | ? | 4 | ? | 6 | 6 | 2 | * | 2 | 2 | 3 | ? | 26 | 2 | 8 |
| S | 2 | 2 | 3 | 3 | 2 | 9 | 3 | 2 | 2 | 16 | 2 | 6 | ? | 3 | 2 | 2 | 2 | * | 4 | 4 | ? | 2 | 2 | 2 |
| T | 6 | 2 | 2 | 6 | 3 | 2 | 2 | 6 | 36 | ? | 4 | 2 | ? | ? | 6 | 4 | 2 | 4 | * | 6 | ? | 6 | 2 | 3 |
| U | 6 | ? | 6 | 4 | ? | 4 | ? | 2 | 4 | 4 | ? | ? | ? | ? | 3 | 4 | 3 | 4 | 6 | * | ? | 6 | ? | 6 |
| V | 3 | ? | 2 | 3 | ? | ? | ? | ? | ? | 3 | ? | ? | ? | 2 | 3 | ? | ? | ? | ? | ? | * | ? | ? | 3 |
| X | 6 | ? | 4 | 6 | 12 | ? | ? | 2 | ? | ? | ? | ? | ? | ? | 2 | ? | 26 | 2 | 6 | 6 | ? | * | 3 | 2 |
| Y | 20 | 8 | 2 | 6 | 2 | 2 | 2 | 28 | 2 | 2 | ? | ? | ? | ? | 2 | 10 | 2 | 2 | 2 | ? | ? | 3 | * | 2 |
| Z | 3 | 4 | 6 | 3 | 2 | 3 | 4 | 2 | 2 | 2 | ? | 10 | 2 | 2 | 2 | 2 | 8 | 2 | 3 | 6 | 3 | 2 | 2 | * |
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | P | Q | R | S | T | U | V | X | Y | Z |